
 4:32
4:32
2025-02-17 16:00

 12:56
12:56

 12:56
12:56
2022-10-25 16:49

 5:02
5:02

 5:02
5:02
Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)
2024-11-23 06:00

 12:02
12:02

 12:02
12:02
2024-09-10 13:14

 9:41
9:41

 9:41
9:41
2024-10-29 15:00

 4:26
4:26

 4:26
4:26
2025-03-22 09:00

 7:46
7:46

 7:46
7:46
2023-12-06 14:30

 15:50
15:50

 15:50
15:50
2024-09-21 20:37

 10:55
10:55

 10:55
10:55
2022-03-03 11:00

 43:10
43:10

 43:10
43:10
2024-10-20 14:13

 4:31
4:31

 4:31
4:31
2023-09-27 09:43
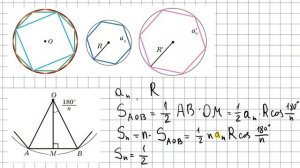
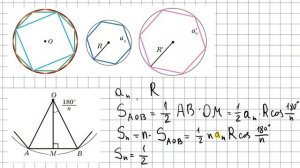 11:17
11:17
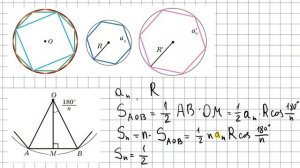
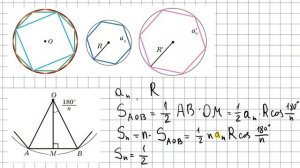 11:17
11:17
2025-05-09 01:05

 18:23
18:23

 18:23
18:23
2024-09-25 00:01
 2:59
2:59

 2:59
2:59
2023-09-24 22:06

 9:25
9:25

 9:25
9:25
2024-06-04 08:25

 6:04
6:04

 6:04
6:04
2024-12-05 23:51

 1:29:02
1:29:02
![Григорий Герасимов - Бутылка крепкого вина (Премьера клипа 2026)]() 3:13
3:13
![TOMA - Заберу (Премьера клипа 2026)]() 2:55
2:55
![Антон и Альфия - Январская вьюга (Премьера клипа 2026)]() 3:32
3:32
![Женя Белоусова - Кричать (Премьера клипа 2026)]() 3:33
3:33
![Зульфия Чотчаева - Снежинки (Премьера клипа 2026)]() 3:08
3:08
![Клава Кока - Тысячи зим (Премьера клипа 2026)]() 2:44
2:44
![Jazzdauren - Юность (Премьера клипа 2026)]() 2:44
2:44
![Эльдар Долаев - Моя стервочка (Премьера клипа 2026)]() 3:10
3:10
![МАРАТ & АРНИ - Надо ли (Премьера клипа 2026)]() 2:36
2:36
![NAIMAN - Тебя украду (Премьера клипа 2026)]() 2:28
2:28
![Ozoda - O'rnimda bo'lsang (Official Video 2026)]() 5:38
5:38
![БАХТАВАР - В белом платье (Премьера клипа 2026)]() 3:17
3:17
![Оксана Ковалевская - Ты меня не ищи (Премьера клипа 2026)]() 3:05
3:05
![Руслан Жароков - Цвета неба (Премьера клипа 2026)]() 4:02
4:02
![Ислам Мальсуйгенов - Ледяное сердце (Премьера клипа 2026)]() 2:30
2:30
![Руслан Добрый - Загадка (Премьера клипа 2026)]() 2:16
2:16
![Cvetocek7 - Нежность (Премьера клипа 2026)]() 2:34
2:34
![Жалолиддин Ахмадалиев - Хеч одам булмайди бази бировлар (Премьера клипа 2026)]() 3:22
3:22
![Алишер Файз - Биё-биё (Премьера клипа 2026)]() 3:16
3:16
![Инна Вальтер - Ты любишь петь (Премьера клипа 2026)]() 3:49
3:49
![Тихое место: День первый | A Quiet Place: Day One (2024)]() 1:39:30
1:39:30
![Мелодия их мечты | Song Sung Blue (2025)]() 2:12:15
2:12:15
![Миссия невыполнима: Смертельная расплата | Mission: Impossible - Dead Reckoning (2023)]() 2:46:48
2:46:48
![Лакомый кусок | The Rip (2026)]() 1:52:50
1:52:50
![Астронавт | The Astronaut (2025)]() 1:30:31
1:30:31
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Игры Биста. 2 сезон, 1 серия | Beast Games 2 season]() 43:55
43:55
![Новокаин | Novocaine (2025)]() 1:49:34
1:49:34
![Всемирный потоп | Daehongsu (2025)]() 1:48:57
1:48:57
![Гарри Поттер и узник Азкабана | Harry Potter and the Prisoner of Azkaban (2004)]() 2:21:46
2:21:46
![Гарри Поттер и Дары Смерти: Часть I | Harry Potter and the Deathly Hallows - Part 1 (2010)]() 2:26:10
2:26:10
![Игры Биста. 2 сезон, 5 серия | Beast Games 2 season]() 49:20
49:20
![Опасный дуэт | The Wrecking Crew (2026)]() 2:04:21
2:04:21
![Носферату | Nosferatu (2024)]() 2:12:40
2:12:40
![Орудия | Weapons (2025)]() 2:08:34
2:08:34
![Давид | David (2025)]() 1:49:18
1:49:18
![Претенденты | Challengers (2024)]() 2:11:42
2:11:42
![Иерархия | Hierarchy (2025)]() 1:39:35
1:39:35
![Гарри Поттер и философский камень | Harry Potter and the Sorcerer's Stone (2001)]() 2:32:26
2:32:26
![Миссия невыполнима: Финальная расплата | Mission: Impossible - The Final Reckoning (2025)]() 2:52:58
2:52:58
![Папа Супергерой Сезон 1]() 4:28
4:28
![Корги по имени Моко. Волшебный мир снов]() 8:60
8:60
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Пластилинки]() 25:31
25:31
![Мультфильмы военных лет | Специальный проект к 80-летию Победы]() 7:20
7:20
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Последний книжный магазин]() 11:20
11:20
![Мотофайтеры]() 13:10
13:10
![Умка]() 7:11
7:11
![Приключения Тайо]() 12:50
12:50
![Лудлвилль]() 7:05
7:05
![Псэмми. Пять детей и волшебство Сезон 1]() 12:17
12:17
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:46
10:46
![Оранжевая корова]() 6:30
6:30
![Тодли Великолепный!]() 3:15
3:15
![Сборники «Простоквашино»]() 1:05:30
1:05:30
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Рэй и пожарный патруль Сезон 1]() 13:27
13:27
![Сборники «Ну, погоди!»]() 1:10:01
1:10:01
![Агент 203]() 21:08
21:08
![Цып-Цып - Мультики для детей - Все серии подряд!]() 1:45:28
1:45:28
![Сборник На Кухне | Уральские Пельмени]() 1:30:27
1:30:27
![Антиреспект - Тишины хочу]() 4:33
4:33
![Сборник Синий Трактор]() 57:36
57:36
![КЛИПЫ 90х ⭐Русский Сборник видеоклипов]() 2:54:39
2:54:39
![СваТы 1 сезон(все серии)]() 2:17:36
2:17:36
![Три Кота 🐱 Сборник серий подряд | Смотреть онлайн развивающие мультики и игры для детей и малышей]() 3:16:51
3:16:51
![Штрафбат(1-11 серии) HD 2004]() 8:05:56
8:05:56
![Барбоскины 1-30]() 2:21:36
2:21:36
![Дева и дракон | Damsel (2024)]() 1:49:38
1:49:38
![ХИТЫ 2025 ТАНЦЕВАЛЬНАЯ МУЗЫКА СБОРНИК]() 1:41:18
1:41:18
![Аватар: Путь воды (2022)]() 3:12:39
3:12:39
![Три Кота | Сборник замечательных серий | Мультфильмы для детей😃]() 1:03:03
1:03:03
![ЛУЧШИЕ ВИДЕО КЛИПЫ 80-90-х. Звёзды Эстрады. Золотые хиты. Супердискотека.]() 2:56:03
2:56:03
![Бандитский Петербург. Все серии подряд. 60fps]() 66:54:01
66:54:01
![Сборник Топ 20 Номеров за 2024 год - Уральские Пельмени]() 2:52:30
2:52:30
![50 клипов шансона]() 3:12:53
3:12:53
![КАМИН 4К 🔥 FIREPLACE 4K | Звуки камина и Треск огня]() 2:00:00
2:00:00
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Лунтик | Танцы 💃💃💃 Сборник мультиков для детей]() 46:30
46:30

 1:29:02
1:29:02Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:13
3:13
2026-02-08 12:57
 2:55
2:55
2026-02-02 10:04
 3:32
3:32
2026-01-28 09:47
 3:33
3:33
2026-02-08 12:36
 3:08
3:08
2026-02-08 13:19
 2:44
2:44
2026-01-30 18:37
 2:44
2:44
2026-01-28 11:45
 3:10
3:10
2026-02-07 13:06
 2:36
2:36
2026-02-04 10:45
 2:28
2:28
2026-01-28 12:37
 5:38
5:38
2026-02-07 12:54
 3:17
3:17
2026-01-28 09:57
 3:05
3:05
2026-01-24 13:42
 4:02
4:02
2026-02-02 16:53
 2:30
2:30
2026-01-24 13:36
 2:16
2:16
2026-02-08 13:12
 2:34
2:34
2026-02-08 13:05
 3:22
3:22
2026-02-07 13:11
 3:16
3:16
2026-01-28 11:55
 3:49
3:49
2026-01-28 10:32
0/0
 1:39:30
1:39:30
2026-01-23 18:43
 2:12:15
2:12:15
2026-01-21 16:23
 2:46:48
2:46:48
2026-01-23 18:43
 1:52:50
1:52:50
2026-01-23 09:26
 1:30:31
1:30:31
2026-01-14 15:48
 1:47:36
1:47:36
2025-12-25 17:49
 43:55
43:55
2026-01-07 23:47
 1:49:34
1:49:34
2026-01-23 18:44
 1:48:57
1:48:57
2026-01-14 15:48
 2:21:46
2:21:46
2025-12-25 15:40
 2:26:10
2:26:10
2025-12-25 15:40
 49:20
49:20
2026-01-23 13:36
 2:04:21
2:04:21
2026-02-02 00:43
 2:12:40
2:12:40
2026-01-23 18:44
 2:08:34
2:08:34
2026-01-23 18:44
 1:49:18
1:49:18
2026-01-29 11:25
 2:11:42
2:11:42
2026-01-23 18:43
 1:39:35
1:39:35
2026-02-06 18:40
 2:32:26
2:32:26
2025-12-25 15:41
 2:52:58
2:52:58
2026-01-23 19:12
0/0
2021-09-22 21:52
 8:60
8:60
2025-12-09 11:58
2021-09-22 22:45
 25:31
25:31
2022-04-01 14:30
 7:20
7:20
2025-05-03 12:34
2021-09-22 20:39
 11:20
11:20
2025-09-12 10:05
 13:10
13:10
2024-11-27 14:57
 7:11
7:11
2026-01-20 10:00
 12:50
12:50
2024-12-17 13:25
 7:05
7:05
2025-12-30 20:49
2021-09-22 22:23
 10:46
10:46
2022-06-07 11:02
 6:30
6:30
2025-12-30 19:54
 3:15
3:15
2025-06-10 13:56
 1:05:30
1:05:30
2025-06-27 13:20
 13:00
13:00
2024-11-28 16:19
2021-09-22 23:51
 1:10:01
1:10:01
2025-07-25 20:16
 21:08
21:08
2025-01-09 16:39
0/0
Скачать популярное видео
Популярное видео
2022-06-06 09:02
2025-04-04 18:26
 4:33
4:33
2019-12-02 21:15
2024-11-13 13:06
2022-03-11 11:17
2025-07-24 20:55
 3:16:51
3:16:51
2025-10-03 19:48
2017-07-08 19:33
2024-12-16 20:15
 1:49:38
1:49:38
2024-03-12 00:19
2024-06-25 00:21
2025-06-17 19:00
 1:03:03
1:03:03
2026-02-02 23:42
2021-03-15 02:49
2023-05-15 17:30
2025-01-13 14:00
2022-12-22 16:10
2024-12-19 00:00
 1:47:25
1:47:25
2025-11-27 03:58
2024-08-05 22:22
0/0

