
 3:55
3:55
2025-01-15 08:18

 6:56
6:56

 6:56
6:56
2024-10-18 05:21
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14
2025-09-23 12:00

 2:09
2:09

 2:09
2:09
2023-12-04 12:15

 16:17
16:17

 16:17
16:17
2025-09-17 18:32
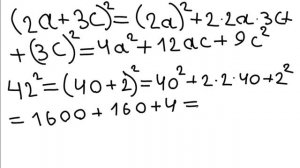
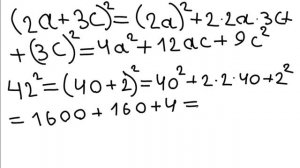 10:23
10:23
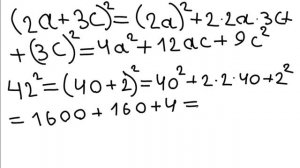
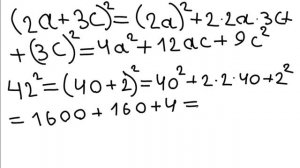 10:23
10:23
2025-02-19 16:17

 10:29
10:29

 10:29
10:29
2025-09-22 09:39
 8:15
8:15
 8:15
8:15
2025-02-17 08:20

 5:52
5:52

 5:52
5:52
2025-09-25 23:50

 34:56
34:56

 34:56
34:56
2025-09-12 16:44

 27:58
27:58

 27:58
27:58
2025-09-20 10:00

 13:45
13:45

 13:45
13:45
2023-11-05 13:00
 4:42
4:42

 4:42
4:42
2023-09-13 11:32

 8:30
8:30

 8:30
8:30
2025-09-12 15:00

 3:20
3:20

 3:20
3:20
2025-09-11 10:37

 1:57:38
1:57:38

 1:57:38
1:57:38
2025-09-15 15:22

 23:31
23:31

 23:31
23:31
2025-09-28 11:00

 1:06:32
1:06:32
![Мухит Бобоев - Маликам (Премьера клипа 2025)]() 3:18
3:18
![NYUSHA, ChinKong - Непогода (Премьера клипа 2025)]() 3:17
3:17
![Амина Магомедова - Не пара (Премьера 2025)]() 3:40
3:40
![Enrasta - За тобой (Премьера клипа 2025)]() 2:41
2:41
![Tural Everest, Baarni - Ушедший покой (Премьера клипа 2025)]() 3:01
3:01
![Слава - В сердце бьёт молния (Премьера клипа 2025)]() 3:30
3:30
![Руслан Добрый - Тёплые края (Премьера клипа 2025)]() 2:14
2:14
![KAYA - Девочки, отмена (Премьера клипа 2025)]() 3:53
3:53
![Жамхур Хайруллаев - Битта дона (Премьера клипа 2025)]() 2:49
2:49
![Надежда Мельянцева - Котёнок, не плачь (Премьера клипа 2025)]() 3:02
3:02
![Бобур Ахмад - Куролмаслар (Премьера клипа 2025)]() 3:33
3:33
![Тахмина Умалатова - Не потеряй (Премьера клипа 2025)]() 4:10
4:10
![Magas - Только ты (Премьера клипа 2025)]() 3:04
3:04
![МАРАТ & АРНИ - Я ЖЕНИЛСЯ (Премьера клипа 2025)]() 4:16
4:16
![Соня Белькевич, Олег Семенов - Увы, мадам (Премьера 2025)]() 3:33
3:33
![Bruno Mars ft. Ed Sheeran – Home to You (Official Video 2025)]() 3:25
3:25
![Равшанбек Балтаев - Кастюм (Премьера клипа 2025)]() 3:59
3:59
![Иброхим Уткиров - Коракуз (Премьера клипа 2025)]() 4:28
4:28
![Анжелика Агурбаш - Утро (Премьера клипа 2025)]() 3:33
3:33
![ESCO - За тобой (Премьера клипа 2025)]() 2:13
2:13
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Бешеные псы | Reservoir Dogs (1991) (Гоблин)]() 1:39:10
1:39:10
![Баллада о маленьком игроке | Ballad of a Small Player (2025)]() 1:42:60
1:42:60
![Хищник | Predator (1987) (Гоблин)]() 1:46:40
1:46:40
![Плохой Cанта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:28:32
1:28:32
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Цельнометаллическая оболочка | Full Metal Jacket (1987) (Гоблин)]() 1:56:34
1:56:34
![Свинтусы | The Twits (2025)]() 1:42:50
1:42:50
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Не грози Южному Централу, попивая сок у себя в квартале | Don't Be a Menace to South Central (1995) (Гоблин)]() 1:28:57
1:28:57
![Рок-н-рольщик | RocknRolla (2008) (Гоблин)]() 1:54:23
1:54:23
![Криминальное чтиво | Pulp Fiction (1994) (Гоблин)]() 2:32:48
2:32:48
![Большой куш / Спи#дили | Snatch (2000) (Гоблин)]() 1:42:50
1:42:50
![Трон: Арес | Tron: Ares (2025)]() 1:52:27
1:52:27
![Крушащая машина | The Smashing Machine (2025)]() 2:03:12
2:03:12
![От заката до рассвета | From Dusk Till Dawn (1995) (Гоблин)]() 1:47:54
1:47:54
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Кей-поп-охотницы на демонов | KPop Demon Hunters (2025)]() 1:39:41
1:39:41
![Только ты | All of You (2025)]() 1:38:22
1:38:22
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Кадеты Баданаму Сезон 1]() 11:50
11:50
![Супер Зак]() 11:38
11:38
![Крутиксы]() 11:00
11:00
![Тодли Великолепный!]() 3:15
3:15
![Пип и Альба Сезон 1]() 11:02
11:02
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Енотки]() 7:04
7:04
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Сборники «Оранжевая корова»]() 1:05:15
1:05:15
![Монсики]() 6:30
6:30
![Тайны Медовой долины]() 7:01
7:01
![Приключения Пети и Волка]() 11:00
11:00
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Чемпионы]() 7:35
7:35
![МегаМен: Полный заряд Сезон 1]() 10:42
10:42
![Панда и петушок Лука]() 12:12
12:12
![Приключения Тайо]() 12:50
12:50
![Истории Баданаму Сезон 1]() 10:02
10:02

 1:06:32
1:06:32Скачать видео
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:18
3:18
2025-11-02 10:30
 3:17
3:17
2025-11-07 13:37
 3:40
3:40
2025-11-05 00:22
 2:41
2:41
2025-11-07 14:04
 3:01
3:01
2025-10-31 13:49
 3:30
3:30
2025-11-02 09:52
 2:14
2:14
2025-11-05 00:29
 3:53
3:53
2025-11-06 12:59
 2:49
2:49
2025-11-06 13:20
 3:02
3:02
2025-10-31 12:43
 3:33
3:33
2025-11-02 10:17
 4:10
4:10
2025-11-06 11:31
 3:04
3:04
2025-11-05 00:49
 4:16
4:16
2025-11-06 13:11
 3:33
3:33
2025-11-07 15:10
 3:25
3:25
2025-11-02 10:34
 3:59
3:59
2025-11-04 18:03
 4:28
4:28
2025-11-03 15:38
 3:33
3:33
2025-11-02 10:06
 2:13
2:13
2025-10-31 12:20
0/0
 2:15:54
2:15:54
2025-10-13 19:02
 1:39:10
1:39:10
2025-09-23 22:53
 1:42:60
1:42:60
2025-10-31 10:53
 1:46:40
1:46:40
2025-10-07 09:27
 1:28:32
1:28:32
2025-10-07 09:27
 2:02:20
2:02:20
2025-10-01 12:06
 1:35:11
1:35:11
2025-10-13 12:06
 1:56:34
1:56:34
2025-09-23 22:53
 1:42:50
1:42:50
2025-10-21 16:19
 1:54:40
1:54:40
2025-09-24 11:35
 1:28:57
1:28:57
2025-09-23 22:52
 1:54:23
1:54:23
2025-09-23 22:53
 2:32:48
2:32:48
2025-09-23 22:52
 1:42:50
1:42:50
2025-09-23 22:53
 1:52:27
1:52:27
2025-11-06 18:12
 2:03:12
2:03:12
2025-11-07 20:11
 1:47:54
1:47:54
2025-09-23 22:53
 2:09:55
2:09:55
2025-10-05 00:32
 1:39:41
1:39:41
2025-10-29 16:30
 1:38:22
1:38:22
2025-10-01 12:16
0/0
2021-09-22 21:03
2021-09-22 21:17
2021-09-22 22:07
 11:00
11:00
2022-07-25 18:59
 3:15
3:15
2025-06-10 13:56
2021-09-22 23:37
2021-09-22 22:45
 7:04
7:04
2022-03-29 18:22
2021-09-22 20:39
 3:28
3:28
2025-01-09 17:01
 1:05:15
1:05:15
2025-09-30 13:45
 6:30
6:30
2022-03-29 19:16
 7:01
7:01
2022-03-30 17:25
 11:00
11:00
2022-04-01 17:59
2021-09-22 23:36
 7:35
7:35
2025-11-01 09:00
2021-09-22 21:43
 12:12
12:12
2024-11-29 14:21
 12:50
12:50
2024-12-17 13:25
2021-09-22 21:29
0/0

