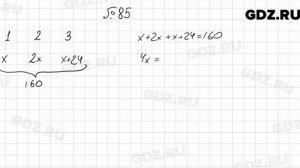
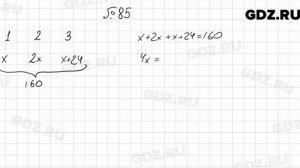 1:52
1:52
2023-12-16 23:52

 13:06
13:06

 13:06
13:06
2024-11-12 21:03

 7:11
7:11

 7:11
7:11
2024-10-26 04:44

 8:51
8:51

 8:51
8:51
2024-09-10 13:43

 7:49
7:49

 7:49
7:49
2024-09-10 13:43
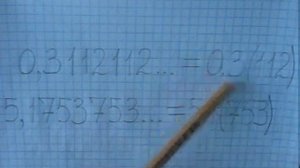
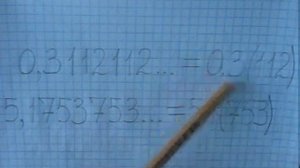 0:39
0:39
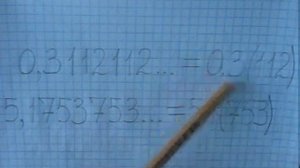
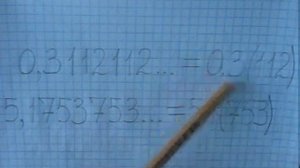 0:39
0:39
2024-01-11 17:39

 10:42
10:42

 10:42
10:42
2025-09-22 12:59

 4:32
4:32

 4:32
4:32
2024-10-26 05:26

 10:19
10:19

 10:19
10:19
2025-09-05 13:35

 10:06
10:06

 10:06
10:06
2025-09-09 21:02

 10:11
10:11

 10:11
10:11
2025-09-17 18:02

 6:55
6:55

 6:55
6:55
2025-02-22 08:01

 7:19
7:19

 7:19
7:19
2025-09-24 15:35
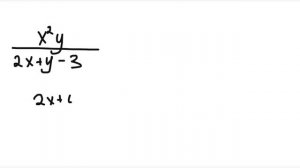
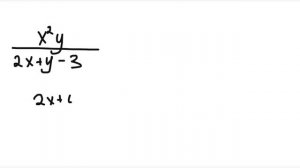 5:46
5:46
 5:46
5:46
2025-02-22 08:57

 8:30
8:30

 8:30
8:30
2025-02-15 19:58

 5:52
5:52

 5:52
5:52
2025-09-25 23:50

 1:23:24
1:23:24

 1:23:24
1:23:24
2025-09-18 12:00

 34:56
34:56
![ESCO - За тобой (Премьера клипа 2025)]() 2:13
2:13
![Tamo ft Djan Edmonte - Ну что красавица (Премьера клипа 2025)]() 3:10
3:10
![A'Studio – Она не виновата (Премьера клипа 2025)]() 2:13
2:13
![Абдуллах Борлаков, Мекка Борлакова - Звездная ночь (Премьера клипа 2025)]() 4:25
4:25
![Антон Макарский - Не уходи (Премьера клипа 2025)]() 3:41
3:41
![Анжелика Агурбаш - Утро (Премьера клипа 2025)]() 3:33
3:33
![NYUSHA, ChinKong - Непогода (Премьера клипа 2025)]() 3:17
3:17
![EDGAR - Мой брат (Премьера клипа 2025)]() 3:33
3:33
![Жамхур Хайруллаев - Битта дона (Премьера клипа 2025)]() 2:49
2:49
![Вусал Мирзаев - Слов не надо (Премьера клипа 2025)]() 2:19
2:19
![Bruno Mars ft. Ed Sheeran – Home to You (Official Video 2025)]() 3:25
3:25
![Илёс Юнусий - Каранг она якинларим (Премьера клипа 2025)]() 3:36
3:36
![Roza Zərgərli, Мурад Байкаев - Неизбежная любовь (Премьера клипа 2025)]() 2:34
2:34
![Марина Хлебникова, Russell Ray - Солнышко (Премьера клипа 2025)]() 4:42
4:42
![NIKA DUBIK, Winter Spirit - Искры (Премьера клипа 2025)]() 4:27
4:27
![Руслан Добрый - Тёплые края (Премьера клипа 2025)]() 2:14
2:14
![Gulinur - Nishatar (Official Video 2025)]() 3:40
3:40
![BITTUEV - Не плачь (Премьера клипа 2025)]() 2:18
2:18
![Бобур Ахмад - Куролмаслар (Премьера клипа 2025)]() 3:33
3:33
![Enrasta - За тобой (Премьера клипа 2025)]() 2:41
2:41
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Диспетчер | Relay (2025)]() 1:51:56
1:51:56
![Криминальное чтиво | Pulp Fiction (1994) (Гоблин)]() 2:32:48
2:32:48
![Большой куш / Спи#дили | Snatch (2000) (Гоблин)]() 1:42:50
1:42:50
![Шматрица | The Matrix (1999) (Гоблин)]() 2:17:10
2:17:10
![Однажды в Ирландии | The Guard (2011) (Гоблин)]() 1:32:16
1:32:16
![Бешеные псы | Reservoir Dogs (1991) (Гоблин)]() 1:39:10
1:39:10
![Рок-н-рольщик | RocknRolla (2008) (Гоблин)]() 1:54:23
1:54:23
![Отчаянный | Desperado (1995) (Гоблин)]() 1:40:18
1:40:18
![Вальсируя с Брандо | Waltzing with Brando (2024)]() 1:44:15
1:44:15
![Гедда | Hedda (2025)]() 1:48:23
1:48:23
![Цельнометаллическая оболочка | Full Metal Jacket (1987) (Гоблин)]() 1:56:34
1:56:34
![Карты, деньги, два ствола | Lock, Stock and Two Smoking Barrels (1998) (Гоблин)]() 1:47:27
1:47:27
![Большой Лебовски | The Big Lebowski (1998) (Гоблин)]() 1:56:59
1:56:59
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Чёрный телефон 2 | Black Phone 2 (2025)]() 1:53:55
1:53:55
![Свинтусы | The Twits (2025)]() 1:42:50
1:42:50
![От заката до рассвета | From Dusk Till Dawn (1995) (Гоблин)]() 1:47:54
1:47:54
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Пиратская школа]() 11:06
11:06
![Панда и петушок Лука]() 12:12
12:12
![Истории Баданаму Сезон 1]() 10:02
10:02
![Сборники «Простоквашино»]() 1:05:35
1:05:35
![Забавные медвежата]() 13:00
13:00
![Команда Дино Сезон 1]() 12:08
12:08
![Пингвиненок Пороро]() 7:42
7:42
![Пип и Альба Сезон 1]() 11:02
11:02
![Лудлвилль]() 7:09
7:09
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Умка]() 7:11
7:11
![Зебра в клеточку]() 6:30
6:30
![Папа Супергерой Сезон 1]() 4:28
4:28
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:21
10:21
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Люк - путешественник во времени]() 1:19:50
1:19:50
![Паровозик Титипо]() 13:42
13:42
![Енотки]() 7:04
7:04
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24

 34:56
34:56Скачать видео
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 2:13
2:13
2025-10-31 12:20
 3:10
3:10
2025-11-07 13:57
 2:13
2:13
2025-10-31 12:53
 4:25
4:25
2025-11-07 13:49
 3:41
3:41
2025-11-05 11:55
 3:33
3:33
2025-11-02 10:06
 3:17
3:17
2025-11-07 13:37
 3:33
3:33
2025-11-07 13:31
 2:49
2:49
2025-11-06 13:20
 2:19
2:19
2025-11-07 14:25
 3:25
3:25
2025-11-02 10:34
 3:36
3:36
2025-11-02 10:25
 2:34
2:34
2025-11-05 11:45
 4:42
4:42
2025-11-06 13:16
 4:27
4:27
2025-10-31 16:00
 2:14
2:14
2025-11-05 00:29
 3:40
3:40
2025-10-31 13:38
 2:18
2:18
2025-10-31 15:53
 3:33
3:33
2025-11-02 10:17
 2:41
2:41
2025-11-07 14:04
0/0
 1:35:11
1:35:11
2025-10-13 12:06
 1:51:56
1:51:56
2025-09-24 11:35
 2:32:48
2:32:48
2025-09-23 22:52
 1:42:50
1:42:50
2025-09-23 22:53
 2:17:10
2:17:10
2025-09-23 22:53
 1:32:16
1:32:16
2025-09-23 22:53
 1:39:10
1:39:10
2025-09-23 22:53
 1:54:23
1:54:23
2025-09-23 22:53
 1:40:18
1:40:18
2025-09-23 22:53
 1:44:15
1:44:15
2025-11-07 20:19
 1:48:23
1:48:23
2025-11-05 19:47
 1:56:34
1:56:34
2025-09-23 22:53
 1:47:27
1:47:27
2025-09-23 22:52
 1:56:59
1:56:59
2025-09-23 22:53
 2:02:20
2:02:20
2025-10-01 12:06
 1:53:55
1:53:55
2025-11-05 19:47
 1:42:50
1:42:50
2025-10-21 16:19
 1:47:54
1:47:54
2025-09-23 22:53
 2:09:55
2:09:55
2025-10-05 00:32
 1:54:40
1:54:40
2025-09-24 11:35
0/0
 11:06
11:06
2022-04-01 15:56
 12:12
12:12
2024-11-29 14:21
2021-09-22 21:29
 1:05:35
1:05:35
2025-10-31 17:03
 13:00
13:00
2024-12-02 13:15
2021-09-22 22:29
 7:42
7:42
2024-12-17 12:21
2021-09-22 23:37
 7:09
7:09
2023-07-06 19:20
2021-09-22 23:36
 7:11
7:11
2025-01-13 11:05
 6:30
6:30
2022-03-31 13:09
2021-09-22 21:52
 6:30
6:30
2018-04-03 10:35
 10:21
10:21
2025-09-11 10:05
 4:33
4:33
2024-12-17 16:56
 1:19:50
1:19:50
2024-12-17 16:00
 13:42
13:42
2024-11-28 14:12
 7:04
7:04
2022-03-29 18:22
 12:24
12:24
2024-11-27 13:24
0/0
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
