
 5:40
5:40
2024-12-01 12:00

 5:30
5:30

 5:30
5:30
2024-12-01 10:30

 9:37
9:37

 9:37
9:37
2023-12-06 14:30

 38:01
38:01

 38:01
38:01
2026-02-26 11:00

 10:10
10:10

 10:10
10:10
2024-09-15 09:23

 3:36
3:36

 3:36
3:36
2024-12-01 08:30

 4:57
4:57

 4:57
4:57
2024-11-01 16:30

 6:05
6:05

 6:05
6:05
2025-02-12 17:30
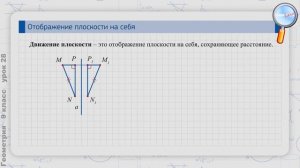
 4:15
4:15

 4:15
4:15
2023-12-22 05:17

 4:26
4:26

 4:26
4:26
2025-02-03 17:15

 4:15
4:15

 4:15
4:15
2024-01-03 14:56

 1:52
1:52

 1:52
1:52
2023-02-02 21:58

 4:38
4:38

 4:38
4:38
2013-11-16 04:49

 16:53
16:53

 16:53
16:53
2024-08-22 10:16
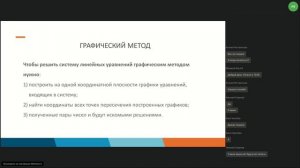
 30:40
30:40

 30:40
30:40
2023-12-02 03:50
 13:04
13:04

 13:04
13:04
2024-01-11 17:53
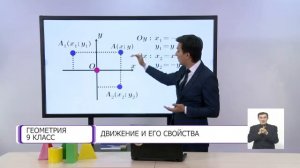
 12:20
12:20

 12:20
12:20
2023-10-07 17:51
 9:16
9:16
![Voydod group - Dilbarijon biyo (Official Video 2026)]() 2:49
2:49
![MONOVIKA - Жить красиво (Премьера клипа 2026)]() 2:30
2:30
![Самир Санаев - Асролмадик (Премьера клипа 2026)]() 4:04
4:04
![Тон Дуэт - Время (Премьера клипа 2026)]() 3:36
3:36
![Enrasta - Не для меня (Премьера клипа 2026)]() 3:38
3:38
![FILIZ KEMAL - HABIBI (Official Video 2026)]() 2:50
2:50
![Сарвар Азим - Ашким (Премьера клипа 2026)]() 3:08
3:08
![DJ Serzh - Аморе мио (Премьера клипа 2026)]() 3:36
3:36
![Ayomiddin Jo'rayev & Mamura Qobilova - Toglarga qor tushganda (Official Video 2026)]() 3:16
3:16
![DOMENICA - PINOKIO (Премьера клипа 2026)]() 3:23
3:23
![Жалолиддин Ахмадалиев - Ёлгон дунё (Премьера клипа 2026)]() 3:44
3:44
![Женя Белоусова - Ты мой (Премьера клипа 2026)]() 3:33
3:33
![Doda - Pamiętnik (Official Video 2026)]() 3:10
3:10
![Manzura - Yuragim ko'nikmaydi (Official Video 2026)]() 4:02
4:02
![Эльдар Агачев - Догорает костер (Премьера клипа 2026)]() 2:23
2:23
![Наталья Влади - Пожелаю тебе (Премьера клипа 2026)]() 2:29
2:29
![Сухроббек Йулдошев - Истанбул (Премьера клипа 2026)]() 3:00
3:00
![Антон и Альфия - Мама, мама (Премьера клипа 2026)]() 3:05
3:05
![MeMaria - Абсолютно всё (Премьера клипа 2026)]() 2:52
2:52
![Artem Smile - Цыганка нагадала (Премьера клипа 2026)]() 2:37
2:37
![Оскар шоу | Oscar Shaw (2025)]() 1:29:22
1:29:22
![Гoрничнaя | The Hоusеmaid (2025)]() 2:11:25
2:11:25
![Игры Биста. 2 сезон, 5 серия | Beast Games 2 season]() 49:20
49:20
![Сущность | The Thing with Feathers (2025)]() 1:38:49
1:38:49
![Лакомый кусок | The Rip (2026)]() 1:52:50
1:52:50
![Претенденты | Challengers (2024)]() 2:11:42
2:11:42
![Опасный дуэт | The Wrecking Crew (2026)]() 2:04:21
2:04:21
![Точка замерзания | Dead of Winter (2025)]() 1:37:45
1:37:45
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Анаконда | Anaconda (2025)]() 1:38:55
1:38:55
![Прощай Джун | Goodbye June (2025)]() 1:56:04
1:56:04
![Спрингстин. Избавь меня от небытия | Springsteen: Deliver Me from Nowhere (2025)]() 1:59:36
1:59:36
![Миссия невыполнима: Финальная расплата | Mission: Impossible - The Final Reckoning (2025)]() 2:52:58
2:52:58
![Пункт назначения: Узы крови | Final Destination: Bloodlines (2025)]() 1:49:52
1:49:52
![Примат | Primate (2025)]() 1:32:11
1:32:11
![Игры Биста. 2 сезон, 4 серия | Beast Games 2 season]() 1:01:10
1:01:10
![Одинокие волки | Wolfs (2024)]() 1:47:12
1:47:12
![Дикий робот | The Wild Robot (2024)]() 1:41:50
1:41:50
![Фэкхем-Холл | Fackham Hall (2025)]() 1:37:17
1:37:17
![Кровь на границе | Frontier Crucible (2025)]() 2:04:36
2:04:36
![Новогодние мультики – Союзмультфильм]() 7:04
7:04
![Роботы-пожарные]() 12:31
12:31
![Мотофайтеры]() 13:10
13:10
![Тайны Медовой долины]() 7:01
7:01
![Сборники «Зебра в клеточку»]() 45:30
45:30
![Зебра в клеточку]() 6:30
6:30
![Хвостатые песенки]() 7:00
7:00
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Минифорс. Сила динозавров]() 12:51
12:51
![Пакман в мире привидений]() 21:37
21:37
![Сборники «Приключения Пети и Волка»]() 1:17:53
1:17:53
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Панда и Антилопа]() 12:08
12:08
![Мультфильмы военных лет | Специальный проект к 80-летию Победы]() 7:20
7:20
![Врумиз. 1 сезон]() 13:10
13:10
![Приключения Тайо]() 12:50
12:50
![Пип и Альба Сезон 1]() 11:02
11:02
![Корги по имени Моко. Волшебный мир снов]() 8:60
8:60
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:46
10:46
![Ну, погоди! Каникулы]() 7:04
7:04
![Дьявол носит Prada | The Devil Wears Prada (2006)]() 1:49:29
1:49:29
![Дева и дракон | Damsel (2024)]() 1:49:38
1:49:38
![Цып-Цып - Мультики для детей - Все серии подряд!]() 1:45:28
1:45:28
![Форсаж 9 | F9 (2021)]() 2:22:56
2:22:56
![Сборник Новогодних Номеров 2024 - Уральские Пельмени]() 3:18:51
3:18:51
![Смешарики (большой сборник)]() 3:25:27
3:25:27
![Гордость и предубеждение | Pride & Prejudice (2005)]() 2:08:21
2:08:21
![Снова в деле (2025) Netflix]() 1:54:23
1:54:23
![ANNA ASTI - ЦАРИЦА ( Премьера клипа 2023 )]() 4:01
4:01
![Винни-Пух. 1969 год.]() 41:23
41:23
![Премьера: Предательство - фильм Андрея Медведева от 01.02.2026]() 59:17
59:17
![Пять ночей с Фредди 2 | Five Nights at Freddy's 2 (2025)]() 1:44:11
1:44:11
![Свои. Баллада о войне [2025, драма, военный]]() 1:29:27
1:29:27
![Bakhtin - Целовала (Премьера клипа 2023)]() 3:16
3:16
![Форсаж 6 | Furious 6 (2013)]() 2:11:07
2:11:07
![Лунтик | Танцы 💃💃💃 Сборник мультиков для детей]() 46:30
46:30
![Барбоскины 1-30]() 2:21:36
2:21:36
![Штрафбат(1-11 серии) HD 2004]() 8:05:56
8:05:56
![Давид | David (2025)]() 1:49:18
1:49:18
![ТОП ЛУЧШИХ КЛИПОВ ШАНСОНА - Слушать шансон лучшее.]() 3:48:45
3:48:45

 9:16
9:16Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 2:49
2:49
2026-02-19 13:17
 2:30
2:30
2026-02-14 11:47
 4:04
4:04
2026-02-14 12:36
 3:36
3:36
2026-02-18 12:03
 3:38
3:38
2026-02-18 17:15
 2:50
2:50
2026-02-18 09:41
 3:08
3:08
2026-02-14 12:48
 3:36
3:36
2026-02-20 09:44
 3:16
3:16
2026-02-18 09:56
 3:23
3:23
2026-02-24 11:00
 3:44
3:44
2026-02-22 22:48
 3:33
3:33
2026-02-20 09:27
 3:10
3:10
2026-02-14 11:53
 4:02
4:02
2026-02-18 10:00
 2:23
2:23
2026-02-16 19:36
 2:29
2:29
2026-02-20 09:20
 3:00
3:00
2026-02-14 12:40
 3:05
3:05
2026-02-18 09:51
 2:52
2:52
2026-02-13 18:08
 2:37
2:37
2026-02-20 20:31
0/0
 1:29:22
1:29:22
2026-01-26 14:34
 2:11:25
2:11:25
2026-02-13 14:02
 49:20
49:20
2026-01-23 13:36
 1:38:49
1:38:49
2026-01-26 14:34
 1:52:50
1:52:50
2026-01-23 09:26
 2:11:42
2:11:42
2026-01-23 18:43
 2:04:21
2:04:21
2026-02-02 00:43
 1:37:45
1:37:45
2026-01-26 14:35
 1:46:45
1:46:45
2026-01-19 12:39
 1:38:55
1:38:55
2026-01-28 12:07
 1:56:04
1:56:04
2026-01-21 16:22
 1:59:36
1:59:36
2026-02-13 14:02
 2:52:58
2:52:58
2026-01-23 19:12
 1:49:52
1:49:52
2026-01-23 18:44
 1:32:11
1:32:11
2026-02-17 21:38
 1:01:10
1:01:10
2026-01-15 03:46
 1:47:12
1:47:12
2026-01-23 18:43
 1:41:50
1:41:50
2026-01-23 18:44
 1:37:17
1:37:17
2026-01-26 14:35
 2:04:36
2:04:36
2026-01-26 14:34
0/0
 7:04
7:04
2023-07-25 00:09
2021-09-23 00:12
 13:10
13:10
2024-11-27 14:57
 7:01
7:01
2022-03-30 17:25
 45:30
45:30
2025-12-11 18:53
 6:30
6:30
2022-03-31 13:09
 7:00
7:00
2025-06-01 11:15
2021-09-22 22:45
 12:51
12:51
2024-11-27 16:39
 21:37
21:37
2024-11-28 17:35
 1:17:53
1:17:53
2025-12-19 23:55
 3:28
3:28
2025-01-09 17:01
 12:08
12:08
2025-06-10 14:59
 7:20
7:20
2025-05-03 12:34
2021-09-24 16:00
 12:50
12:50
2024-12-17 13:25
2021-09-22 23:37
 8:60
8:60
2025-12-09 11:58
 10:46
10:46
2022-06-07 11:02
 7:04
7:04
2026-01-12 15:05
0/0
Скачать популярное видео
Популярное видео
 1:49:29
1:49:29
2023-04-27 15:40
 1:49:38
1:49:38
2024-03-12 00:19
2022-06-06 09:02
 2:22:56
2:22:56
2023-04-25 23:06
2024-12-31 14:00
2025-01-24 05:04
 2:08:21
2:08:21
2023-05-03 20:56
 1:54:23
1:54:23
2025-01-18 20:05
 4:01
4:01
2023-10-12 11:54
2023-11-19 12:01
 59:17
59:17
2026-02-01 14:02
 1:44:11
1:44:11
2025-12-25 22:29
2025-04-11 14:51
 3:16
3:16
2023-10-13 14:26
 2:11:07
2:11:07
2023-04-25 22:52
2024-08-05 22:22
2024-12-16 20:15
 8:05:56
8:05:56
2017-07-08 19:33
 1:49:18
1:49:18
2026-01-29 11:25
2026-02-02 14:57
0/0

