
 4:36
4:36
2023-12-02 12:08

 16:55
16:55

 16:55
16:55
2025-03-28 19:00
 5:07
5:07

 5:07
5:07
2023-12-28 16:03

 2:37
2:37

 2:37
2:37
2024-11-15 04:30

 1:09
1:09

 1:09
1:09
2026-01-17 19:47

 4:11
4:11

 4:11
4:11
2024-11-07 12:00

 2:00
2:00

 2:00
2:00
2025-02-01 09:45
 2:14
2:14

 2:14
2:14
2024-09-17 13:58

 9:21
9:21

 9:21
9:21
2025-04-18 12:00

 4:51
4:51

 4:51
4:51
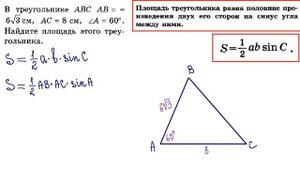
Теорема о площади треугольника по двум сторонам и углу между ними. Доказательство. Геометрия 9 класс
2023-01-21 21:21

 19:30
19:30

 19:30
19:30
2023-01-31 18:32

 1:09
1:09

 1:09
1:09
2025-02-24 19:18

 4:08
4:08

 4:08
4:08
2024-11-19 15:06

 1:55
1:55

 1:55
1:55
2023-12-02 12:00

 18:23
18:23

 18:23
18:23
2023-09-20 05:46

 3:21:60
3:21:60

 3:21:60
3:21:60
2026-01-11 22:40

 11:16:29
11:16:29

 11:16:29
11:16:29
2025-05-23 08:04

 2:58:11
2:58:11
![SOPRANO Турецкого & Кай Син - Ах мамочка, на саночках (Премьера клипа 2026)]() 3:40
3:40
![Жанна Аркадьевна - Ночь в BMW (Премьера клипа 2025)]() 2:09
2:09
![Амина Магомедова - Танцуй со мной (Премьера клипа 2026)]() 3:08
3:08
![Шавкат Зулфикор - Жигарлар (Премьера клипа 2026)]() 5:53
5:53
![Sasha Komovich - Расскажи, Снегурочка (Премьера клипа 2025)]() 2:13
2:13
![Zarina & Jaska Arab - Xo'sh (Official Video 2025)]() 2:54
2:54
![Рустам Батербиев - Стерва-ночь (Премьера клипа 2026)]() 2:24
2:24
![KhaliF - Сияй (Премьера клипа 2026)]() 2:22
2:22
![ANIVAR - Маски (Премьера клипа 2026)]() 2:13
2:13
![Бекзод Жахон - Бухоро (Премьера клипа 2026)]() 4:44
4:44
![Евгений Григорьев ЖЕКА, Алёна Егорова - Синхронит любовь (Премьера клипа 2026)]() 3:24
3:24
![AY YOLA, ALSOU - Ay, bylbylym (Премьера клипа 2026)]() 4:08
4:08
![Elvira T - Don't Cry (Премьера клипа 2026)]() 3:27
3:27
![Илёс Юнусий - Менга ургатманг сиз кандай яшашни (Премьера клипа 2026)]() 3:43
3:43
![Рада Рай - Мечта (Премьера клипа 2025)]() 4:43
4:43
![NAIMAN - Твои глаза (Премьера клипа 2025)]() 2:49
2:49
![DJ Serzh - Котолюция (Премьера клипа 2026)]() 3:30
3:30
![Наталья Влади, Любовь Рыбкина - В жизни успеть (Премьера клипа 2026)]() 2:37
2:37
![Соня Белькевич, ATLANA - Поверь (Премьера 2025)]() 3:59
3:59
![Григорий Герасимов - Я другой (Премьера клипа 2026)]() 3:32
3:32
![Игры Биста. 2 сезон, 2 серия | Beast Games 2 season]() 58:23
58:23
![Один дома 2: Затерянный в Нью-Йорке | Home Alone 2: Lost in New York (1992)]() 2:00:06
2:00:06
![Гедда | Hedda (2025)]() 1:48:23
1:48:23
![Семейный план 2 | The Family Plan 2 (2025)]() 1:46:14
1:46:14
![Мерв | Merv (2025)]() 1:46:56
1:46:56
![Доверие | Trust (2025)]() 1:30:44
1:30:44
![Гарри Поттер и узник Азкабана | Harry Potter and the Prisoner of Azkaban (2004)]() 2:21:46
2:21:46
![Голубая луна | Blue Moon (2025)]() 1:40:33
1:40:33
![Игры Биста. 2 сезон, 5 серия | Beast Games 2 season]() 49:20
49:20
![Игры Биста. 2 сезон, 4 серия | Beast Games 2 season]() 1:01:10
1:01:10
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Один дома | Home Alone (1990)]() 1:43:02
1:43:02
![Астронавт | The Astronaut (2025)]() 1:30:31
1:30:31
![Шматрица | Matrix (1999) (Гоблин)]() 2:17:10
2:17:10
![Гарри Поттер и Дары Смерти: Часть II | Harry Potter and the Deathly Hallows - Part 2 (2011)]() 2:10:30
2:10:30
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Гарри Поттер и философский камень | Harry Potter and the Sorcerer's Stone (2001)]() 2:32:26
2:32:26
![Достать ножи: Воскрешение покойника | Wake Up Dead Man (2025)]() 2:26:20
2:26:20
![Мелодия их мечты | Song Sung Blue (2025)]() 2:12:15
2:12:15
![Зебра в клеточку]() 6:30
6:30
![Ну, погоди! Каникулы]() 7:04
7:04
![Тайны Медовой долины]() 7:01
7:01
![Пакман в мире привидений]() 21:37
21:37
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:46
10:46
![Лудлвилль]() 7:05
7:05
![Сборники «Простоквашино»]() 1:05:30
1:05:30
![Синдбад и семь галактик Сезон 1]() 10:23
10:23
![Чемпионы]() 7:15
7:15
![Корги по имени Моко. Волшебный мир снов]() 8:60
8:60
![Истории Баданаму Сезон 1]() 10:02
10:02
![Агент 203]() 21:08
21:08
![Супер Дино]() 12:41
12:41
![Минифорс. Сила динозавров]() 12:51
12:51
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Врумиз. 1 сезон]() 13:10
13:10
![Чуч-Мяуч]() 7:04
7:04
![Команда Дино Сезон 1]() 12:08
12:08
![Школьный автобус Гордон]() 12:34
12:34

 2:58:11
2:58:11Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 432x232 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:40
3:40
2026-01-20 10:50
 2:09
2:09
2025-12-27 10:14
 3:08
3:08
2026-01-15 13:41
 5:53
5:53
2026-01-10 14:39
 2:13
2:13
2026-01-01 11:00
 2:54
2:54
2025-12-30 19:43
 2:24
2:24
2026-01-15 13:21
 2:22
2:22
2026-01-22 11:38
 2:13
2:13
2026-01-10 14:36
 4:44
4:44
2026-01-04 12:06
 3:24
3:24
2026-01-15 12:53
 4:08
4:08
2026-01-07 22:29
 3:27
3:27
2026-01-08 12:19
 3:43
3:43
2026-01-22 10:47
 4:43
4:43
2025-12-30 11:35
 2:49
2:49
2025-12-26 13:54
 3:30
3:30
2026-01-20 10:30
 2:37
2:37
2026-01-22 10:58
 3:59
3:59
2025-12-28 13:25
 3:32
3:32
2026-01-14 15:22
0/0
 58:23
58:23
2026-01-07 23:52
 2:00:06
2:00:06
2025-12-25 15:39
 1:48:23
1:48:23
2025-11-05 19:47
 1:46:14
1:46:14
2025-11-26 06:44
 1:46:56
1:46:56
2025-12-12 13:56
 1:30:44
1:30:44
2025-12-17 23:52
 2:21:46
2:21:46
2025-12-25 15:40
 1:40:33
1:40:33
2025-12-17 23:52
 49:20
49:20
2026-01-23 13:36
 1:01:10
1:01:10
2026-01-15 03:46
 1:18:55
1:18:55
2025-11-21 14:16
 1:43:02
1:43:02
2025-12-25 15:40
 1:30:31
1:30:31
2026-01-14 15:48
 2:17:10
2:17:10
2025-11-17 12:53
 2:10:30
2:10:30
2025-12-25 15:40
 1:47:25
1:47:25
2025-11-27 03:58
 1:47:36
1:47:36
2025-12-25 17:49
 2:32:26
2:32:26
2025-12-25 15:41
 2:26:20
2:26:20
2025-12-20 21:33
 2:12:15
2:12:15
2026-01-21 16:23
0/0
 6:30
6:30
2022-03-31 13:09
 7:04
7:04
2026-01-12 15:05
 7:01
7:01
2022-03-30 17:25
 21:37
21:37
2024-11-28 17:35
 10:46
10:46
2022-06-07 11:02
 7:05
7:05
2025-12-30 20:49
 1:05:30
1:05:30
2025-06-27 13:20
2021-09-22 23:09
 7:15
7:15
2025-12-10 10:00
 8:60
8:60
2025-12-09 11:58
2021-09-22 21:29
 21:08
21:08
2025-01-09 16:39
 12:41
12:41
2024-11-28 12:54
 12:51
12:51
2024-11-27 16:39
2021-09-22 23:36
2021-09-22 20:39
2021-09-24 16:00
 7:04
7:04
2022-03-29 15:20
2021-09-22 22:29
 12:34
12:34
2024-12-02 14:42
0/0

