
 9:50
9:50
2025-10-22 09:00
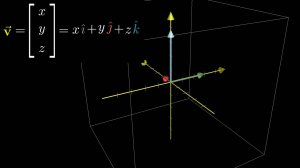
 4:42
4:42

 4:42
4:42
2025-10-24 09:00

 9:55
9:55

 9:55
9:55
2025-10-18 09:00
 1:45
1:45

 1:45
1:45
2023-10-29 00:13
 14:14
14:14

 14:14
14:14
2023-12-05 05:02

 1:33
1:33

 1:33
1:33
2024-04-21 18:24

 1:16:34
1:16:34

 1:16:34
1:16:34
2026-02-25 06:01

 11:52:60
11:52:60

 11:52:60
11:52:60
2025-01-24 09:38

 3:55:20
3:55:20

 3:55:20
3:55:20
2023-11-30 23:17

 2:48:30
2:48:30

 2:48:30
2:48:30
2023-12-23 12:24

 1:44
1:44

 1:44
1:44
2026-02-18 11:59

 11:57:38
11:57:38

 11:57:38
11:57:38
2025-04-23 06:55

 3:02:32
3:02:32

 3:02:32
3:02:32
2023-12-23 12:08

 2:30:39
2:30:39

 2:30:39
2:30:39
2023-12-23 12:22

 44:30
44:30

 44:30
44:30
2025-01-13 21:01

 2:37:05
2:37:05

 2:37:05
2:37:05
2023-09-10 20:03

 10:11:37
10:11:37

 10:11:37
10:11:37
2025-04-07 07:03

 2:21:44
2:21:44
![Максим АРШАВИН - Горько (Премьера клипа 2026)]() 3:09
3:09
![Ayomiddin Jo'rayev & Mamura Qobilova - Toglarga qor tushganda (Official Video 2026)]() 3:16
3:16
![Алишер Абдугофуров - Кизимиз (Премьера клипа 2026)]() 4:20
4:20
![Сухроббек Йулдошев - Истанбул (Премьера клипа 2026)]() 3:00
3:00
![Liana Lee - Глаза-магнит (Премьера клипа 2026)]() 2:01
2:01
![Самир Санаев - Асролмадик (Премьера клипа 2026)]() 4:04
4:04
![Гузэлем - Рамазан (Премьера клипа 2026)]() 2:45
2:45
![NILETTO, Татьяна Буланова - Первыми (Премьера клипа 2026)]() 2:52
2:52
![DAASHA - Сердце на полку (Премьера клипа 2026)]() 2:13
2:13
![Элдор Саматов - Йиглама (Премьера клипа 2026)]() 4:31
4:31
![MONOVIKA - Жить красиво (Премьера клипа 2026)]() 2:30
2:30
![Жалолиддин Ахмадалиев - Ёлгон дунё (Премьера клипа 2026)]() 3:44
3:44
![Эльдар Агачев - Догорает костер (Премьера клипа 2026)]() 2:23
2:23
![Рейсан Магомедкеримов - Опасная (Премьера клипа 2026)]() 3:41
3:41
![FILIZ KEMAL - HABIBI (Official Video 2026)]() 2:50
2:50
![Artem Smile - Цыганка нагадала (Премьера клипа 2026)]() 2:37
2:37
![Alexia - Două Linii (Official Video 2026)]() 2:38
2:38
![Антон и Альфия - Мама, мама (Премьера клипа 2026)]() 3:05
3:05
![Вика Ветер - Ты не забывай меня (Премьера клипа 2026)]() 3:57
3:57
![Тон Дуэт - Время (Премьера клипа 2026)]() 3:36
3:36
![Элла Маккей | Ella McCay (2025)]() 1:54:47
1:54:47
![Миссия невыполнима: Смертельная расплата | Mission: Impossible - Dead Reckoning (2023)]() 2:46:48
2:46:48
![Давид | David (2025)]() 1:49:18
1:49:18
![Тепло наших тел | Warm Bodies (2013)]() 1:37:49
1:37:49
![Лило и Стич | Lilo & Stitch (2025)]() 1:49:28
1:49:28
![Спрингстин. Избавь меня от небытия | Springsteen: Deliver Me from Nowhere (2025)]() 1:59:36
1:59:36
![Побег из плена | Prisoner of War (2025)]() 1:52:58
1:52:58
![Сират | Sirât (2025)]() 1:54:52
1:54:52
![28 лет спустя: Часть II. Храм костей | 28 Years Later: The Bone Temple (2026)]() 1:49:24
1:49:24
![Пункт назначения: Узы крови | Final Destination: Bloodlines (2025)]() 1:49:52
1:49:52
![Семья в аренду | Rental Family (2025)]() 1:49:55
1:49:55
![Оскар шоу | Oscar Shaw (2025)]() 1:29:22
1:29:22
![Дикий робот | The Wild Robot (2024)]() 1:41:50
1:41:50
![Тихое место: День первый | A Quiet Place: Day One (2024)]() 1:39:30
1:39:30
![Отпуск на двоих | People We Meet on Vacation (2026)]() 1:57:55
1:57:55
![Фэкхем-Холл | Fackham Hall (2025)]() 1:37:17
1:37:17
![Сущность | The Thing with Feathers (2025)]() 1:38:49
1:38:49
![Миссия невыполнима: Финальная расплата | Mission: Impossible - The Final Reckoning (2025)]() 2:52:58
2:52:58
![Опасные связи | Bone Lake (2025)]() 1:30:07
1:30:07
![Иерархия | Hierarchy (2025)]() 1:39:35
1:39:35
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Кадеты Баданаму Сезон 1]() 11:50
11:50
![Лудлвилль]() 7:05
7:05
![Сборники «Умка»]() 1:11:53
1:11:53
![Рэй и пожарный патруль Сезон 1]() 13:27
13:27
![Пингвиненок Пороро]() 7:42
7:42
![Команда Дино Сезон 1]() 12:08
12:08
![Пиратская школа]() 11:06
11:06
![Пакман в мире привидений]() 21:37
21:37
![Мультфильмы военных лет | Специальный проект к 80-летию Победы]() 7:20
7:20
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24
![Забавные медвежата]() 13:00
13:00
![Простоквашино. Финансовая грамотность]() 3:27
3:27
![Ну, погоди! Каникулы]() 7:04
7:04
![Корги по имени Моко. Домашние животные]() 1:13
1:13
![МегаМен: Полный заряд Сезон 1]() 10:42
10:42
![Панда и Антилопа]() 12:08
12:08
![Зомби Дамб]() 5:14
5:14
![Чуч-Мяуч]() 7:04
7:04
![Аватар 3: Пламя и пепел фильм, 2025]() 3:09:06
3:09:06
![Три Кота 🐱 Сборник серий подряд | Смотреть онлайн развивающие мультики и игры для детей и малышей]() 3:16:51
3:16:51
![ТОП ЛУЧШИХ КЛИПОВ ШАНСОНА - Слушать шансон лучшее.]() 3:48:45
3:48:45
![КЛИПЫ 90х ⭐Русский Сборник видеоклипов]() 2:54:39
2:54:39
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Гордость и предубеждение | Pride & Prejudice (2005)]() 2:08:21
2:08:21
![_*ДискотекА 80-90х ВиДео АлЬбом Лучшие.*_]() 2:40:60
2:40:60
![MAUR - Полетела (Премьера клипа 2025)]() 2:53
2:53
![Смешарики (большой сборник)]() 3:25:27
3:25:27
![Снова в деле (2025) Netflix]() 1:54:23
1:54:23
![Инна Вальтер - Дымом лечилась (Исповедь хулиганки)]() 7:04
7:04
![Премьера: Предательство - фильм Андрея Медведева от 01.02.2026]() 59:17
59:17
![КАМИН 4К 🔥 FIREPLACE 4K | Звуки камина и Треск огня]() 2:00:00
2:00:00
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Зверополис | Zootopia (2016)]() 1:48:48
1:48:48
![Jakone и Kiliana - Асфальт (Mood Video)]() 2:50
2:50
![Форсаж 9 | F9 (2021)]() 2:22:56
2:22:56
![Аватар: Путь воды (2022)]() 3:12:39
3:12:39
![Сборник Синий Трактор]() 57:36
57:36

 2:21:44
2:21:44Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:09
3:09
2026-02-20 23:46
 3:16
3:16
2026-02-18 09:56
 4:20
4:20
2026-02-25 09:40
 3:00
3:00
2026-02-14 12:40
 2:01
2:01
2026-02-19 13:26
 4:04
4:04
2026-02-14 12:36
 2:45
2:45
2026-02-19 13:22
 2:52
2:52
2026-02-13 17:37
 2:13
2:13
2026-02-20 09:55
 4:31
4:31
2026-02-14 12:43
 2:30
2:30
2026-02-14 11:47
 3:44
3:44
2026-02-22 22:48
 2:23
2:23
2026-02-16 19:36
 3:41
3:41
2026-02-20 09:40
 2:50
2:50
2026-02-18 09:41
 2:37
2:37
2026-02-20 20:31
 2:38
2:38
2026-02-20 10:00
 3:05
3:05
2026-02-18 09:51
 3:57
3:57
2026-02-20 09:52
 3:36
3:36
2026-02-18 12:03
0/0
 1:54:47
1:54:47
2026-02-11 21:47
 2:46:48
2:46:48
2026-01-23 18:43
 1:49:18
1:49:18
2026-01-29 11:25
 1:37:49
1:37:49
2026-02-16 08:53
 1:49:28
1:49:28
2026-01-23 18:44
 1:59:36
1:59:36
2026-02-13 14:02
 1:52:58
1:52:58
2026-01-26 14:34
 1:54:52
1:54:52
2026-01-26 14:35
 1:49:24
1:49:24
2026-02-19 14:08
 1:49:52
1:49:52
2026-01-23 18:44
 1:49:55
1:49:55
2026-02-13 20:27
 1:29:22
1:29:22
2026-01-26 14:34
 1:41:50
1:41:50
2026-01-23 18:44
 1:39:30
1:39:30
2026-01-23 18:43
 1:57:55
1:57:55
2026-01-14 15:48
 1:37:17
1:37:17
2026-01-26 14:35
 1:38:49
1:38:49
2026-01-26 14:34
 2:52:58
2:52:58
2026-01-23 19:12
 1:30:07
1:30:07
2026-02-06 18:40
 1:39:35
1:39:35
2026-02-06 18:40
0/0
2021-09-22 22:45
2021-09-22 21:17
 7:05
7:05
2025-12-30 20:49
 1:11:53
1:11:53
2026-01-29 11:37
2021-09-22 23:51
 7:42
7:42
2024-12-17 12:21
2021-09-22 22:29
 11:06
11:06
2022-04-01 15:56
 21:37
21:37
2024-11-28 17:35
 7:20
7:20
2025-05-03 12:34
 3:28
3:28
2025-01-09 17:01
 12:24
12:24
2024-11-27 13:24
 13:00
13:00
2024-12-02 13:15
 3:27
3:27
2024-12-07 11:00
 7:04
7:04
2026-01-12 15:05
 1:13
1:13
2024-11-29 14:40
2021-09-22 21:43
 12:08
12:08
2025-06-10 14:59
 5:14
5:14
2024-11-28 13:12
 7:04
7:04
2022-03-29 15:20
0/0
Скачать популярное видео
Популярное видео
2025-12-26 16:56
 3:16:51
3:16:51
2025-10-03 19:48
2026-02-02 14:57
2022-03-11 11:17
 1:47:25
1:47:25
2025-11-27 03:58
 2:08:21
2:08:21
2023-05-03 20:56
2024-03-18 17:25
 2:53
2:53
2025-04-24 09:53
2025-01-24 05:04
 1:54:23
1:54:23
2025-01-18 20:05
 7:04
7:04
2018-07-11 11:26
 59:17
59:17
2026-02-01 14:02
2024-12-19 00:00
 1:47:36
1:47:36
2025-12-25 17:49
 2:32:29
2:32:29
2025-11-17 11:22
 1:48:48
1:48:48
2024-12-16 19:01
 2:50
2:50
2024-07-04 15:48
 2:22:56
2:22:56
2023-04-25 23:06
2025-06-17 19:00
2024-11-13 13:06
0/0

