
 5:03
5:03
2025-05-12 16:14

 8:05
8:05

 8:05
8:05
2024-12-29 09:15

 9:15
9:15

 9:15
9:15
2025-04-17 12:57

 27:25
27:25

 27:25
27:25
2026-02-22 16:17

 5:40
5:40

 5:40
5:40
2024-12-21 06:45

 18:41
18:41

 18:41
18:41
2022-03-16 10:43
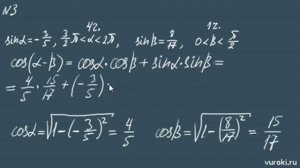
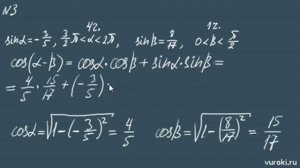 11:29
11:29
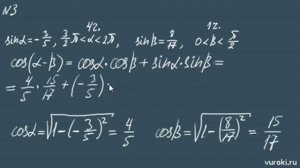
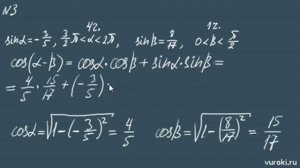 11:29
11:29
2023-12-05 18:09

 10:02
10:02

 10:02
10:02
2024-12-29 11:30

 11:45
11:45

 11:45
11:45
2024-12-29 10:30

 9:15
9:15

 9:15
9:15
2025-08-16 13:12

 43:54
43:54

 43:54
43:54
2023-12-23 01:38

 32:03
32:03

 32:03
32:03
2023-12-17 08:51

 6:36
6:36

 6:36
6:36
2024-09-30 21:34

 3:28
3:28

 3:28
3:28
2022-04-12 09:41

 3:30
3:30

 3:30
3:30
2023-09-03 14:13

 21:28
21:28

 21:28
21:28
2023-09-03 14:45

 2:47
2:47

 2:47
2:47
2024-05-01 22:02

 45:50
45:50
![Самир Санаев - Асролмадик (Премьера клипа 2026)]() 4:04
4:04
![Максим АРШАВИН - Горько (Премьера клипа 2026)]() 3:09
3:09
![БАХТАВАР - RAMADAN (Премьера клипа 2026)]() 3:15
3:15
![Скандальная пара - Душе моей душа нужна (Премьера клипа 2026)]() 3:40
3:40
![Ayomiddin Jo'rayev & Mamura Qobilova - Toglarga qor tushganda (Official Video 2026)]() 3:16
3:16
![Антон и Альфия - Мама, мама (Премьера клипа 2026)]() 3:05
3:05
![KOBZOV - Королева Снежная (Премьера клипа 2026)]() 3:14
3:14
![Voydod group - Dilbarijon biyo (Official Video 2026)]() 2:49
2:49
![Аюбхон Усмонов - Асал (Премьера клипа 2026)]() 3:28
3:28
![Liana Lee - Глаза-магнит (Премьера клипа 2026)]() 2:01
2:01
![Алишер Абдугофуров - Кизимиз (Премьера клипа 2026)]() 4:20
4:20
![Artem Smile - Цыганка нагадала (Премьера клипа 2026)]() 2:37
2:37
![Игорь Кибирев - Разведённые мосты (Премьера клипа 2026)]() 3:22
3:22
![Рустам Батербиев - Пушка (Премьера 2026)]() 3:08
3:08
![Шамиль Каримов - Танцуй малая (Премьера клипа 2026)]() 3:33
3:33
![Эльдар Агачев - Догорает костер (Премьера клипа 2026)]() 2:23
2:23
![DOMENICA - PINOKIO (Премьера клипа 2026)]() 3:23
3:23
![Эстрада шоу гурухи - Шахзодам (Премьера клипа 2026)]() 2:54
2:54
![Ислам Мальсуйгенов, Зульфия Чотчаева - Дарман (Премьера клипа 2026)]() 3:01
3:01
![Enrasta - Не для меня (Премьера клипа 2026)]() 3:38
3:38
![Хамнет: История, вдохновившая «Гамлета» | Hamnet (2025)]() 2:05:47
2:05:47
![Безымянная романтическая история о вторжении в дом | Untitled Home Invasion Romance (2025)]() 1:25:48
1:25:48
![Грандиозная подделка | Il falsario (2025)]() 1:55:41
1:55:41
![Орудия | Weapons (2025)]() 2:08:34
2:08:34
![Тихое место: День первый | A Quiet Place: Day One (2024)]() 1:39:30
1:39:30
![Игры Биста. 2 сезон, 6 серия | Beast Games 2 season]() 1:01:28
1:01:28
![Игры Биста. 2 сезон, 5 серия | Beast Games 2 season]() 49:20
49:20
![Обитель зла: Последняя глава | Resident Evil: The Final Chapter (2016)]() 1:46:38
1:46:38
![Давид | David (2025)]() 1:49:18
1:49:18
![Обитель зла 2: Апокалипсис | Resident Evil: Apocalypse (2004)]() 1:37:50
1:37:50
![Дикий робот | The Wild Robot (2024)]() 1:41:50
1:41:50
![Примат | Primate (2025)]() 1:32:11
1:32:11
![Зомби по имени Шон | Shaun of the Dead (2004)]() 1:39:31
1:39:31
![Обитель зла: Возмездие | Resident Evil: Retribution (2012)]() 1:35:41
1:35:41
![Элла Маккей | Ella McCay (2025)]() 1:54:47
1:54:47
![Претенденты | Challengers (2024)]() 2:11:42
2:11:42
![Носферату | Nosferatu (2024)]() 2:12:40
2:12:40
![Лакомый кусок | The Rip (2025)]() 1:52:50
1:52:50
![Охотник и охотница | Hunting Grounds (2025)]() 1:29:24
1:29:24
![Оскар шоу | Oscar Shaw (2025)]() 1:29:22
1:29:22
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Чемпионы]() 7:15
7:15
![Команда Дино Сезон 1]() 12:08
12:08
![Хвостатые песенки]() 7:00
7:00
![Умка]() 7:11
7:11
![Пластилинки]() 25:31
25:31
![Команда Дино. Исследователи Сезон 2]() 13:26
13:26
![Агент 203]() 21:08
21:08
![Пингвиненок Пороро]() 7:42
7:42
![Сборники «Простоквашино»]() 1:05:30
1:05:30
![Полли Покет Сезон 1]() 21:30
21:30
![Минифорс. Сила динозавров]() 12:51
12:51
![Ну, погоди! Каникулы]() 7:04
7:04
![Мультфильмы военных лет | Специальный проект к 80-летию Победы]() 7:20
7:20
![Чуч-Мяуч]() 7:04
7:04
![Простоквашино. Финансовая грамотность]() 3:27
3:27
![Пиратская школа]() 11:06
11:06
![Лудлвилль]() 7:05
7:05
![Простоквашино]() 7:19
7:19
![Приключения Пети и Волка]() 11:00
11:00
![СваТы 1 сезон(все серии)]() 2:17:36
2:17:36
![ANNA ASTI - ЦАРИЦА ( Премьера клипа 2023 )]() 4:01
4:01
![Jakone и Kiliana - Асфальт (Mood Video)]() 2:50
2:50
![Гордость и предубеждение | Pride & Prejudice (2005)]() 2:08:21
2:08:21
![Сборник Топ 20 Номеров за 2024 год - Уральские Пельмени]() 2:52:30
2:52:30
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Барбоскины 1-30]() 2:21:36
2:21:36
![Форсаж 6 | Furious 6 (2013)]() 2:11:07
2:11:07
![Смешарики (большой сборник)]() 3:25:27
3:25:27
![Инна Вальтер - Дымом лечилась (Исповедь хулиганки)]() 7:04
7:04
![Сборник Новогодних Номеров 2024 - Уральские Пельмени]() 3:18:51
3:18:51
![КЛИПЫ 90х ⭐Русский Сборник видеоклипов]() 2:54:39
2:54:39
![Лунтик | Танцы 💃💃💃 Сборник мультиков для детей]() 46:30
46:30
![MAUR - Полетела (Премьера клипа 2025)]() 2:53
2:53
![Jazzdauren - Дарите женщинам цветы]() 3:09
3:09
![Свои. Баллада о войне [2025, драма, военный]]() 1:29:27
1:29:27
![Аватар: Путь воды (2022)]() 3:12:39
3:12:39
![Пять ночей с Фредди 2 | Five Nights at Freddy's 2 (2025)]() 1:44:11
1:44:11
![Дева и дракон | Damsel (2024)]() 1:49:38
1:49:38
![Премьера: Предательство - фильм Андрея Медведева от 01.02.2026]() 59:17
59:17

 45:50
45:50Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 4:04
4:04
2026-02-14 12:36
 3:09
3:09
2026-02-20 23:46
 3:15
3:15
2026-02-21 14:07
 3:40
3:40
2026-02-19 12:26
 3:16
3:16
2026-02-18 09:56
 3:05
3:05
2026-02-18 09:51
 3:14
3:14
2026-02-19 13:13
 2:49
2:49
2026-02-19 13:17
 3:28
3:28
2026-02-25 09:33
 2:01
2:01
2026-02-19 13:26
 4:20
4:20
2026-02-25 09:40
 2:37
2:37
2026-02-20 20:31
 3:22
3:22
2026-02-25 09:55
 3:08
3:08
2026-02-26 10:16
 3:33
3:33
2026-02-19 13:20
 2:23
2:23
2026-02-16 19:36
 3:23
3:23
2026-02-24 11:00
 2:54
2:54
2026-02-14 12:51
 3:01
3:01
2026-02-20 19:56
 3:38
3:38
2026-02-18 17:15
0/0
 2:05:47
2:05:47
2026-02-06 18:40
 1:25:48
1:25:48
2026-02-26 14:41
 1:55:41
1:55:41
2026-02-26 14:41
 2:08:34
2:08:34
2026-01-23 18:44
 1:39:30
1:39:30
2026-01-23 18:43
 1:01:28
1:01:28
2026-02-04 10:24
 49:20
49:20
2026-01-23 13:36
 1:46:38
1:46:38
2026-02-25 19:41
 1:49:18
1:49:18
2026-01-29 11:25
 1:37:50
1:37:50
2026-02-25 19:41
 1:41:50
1:41:50
2026-01-23 18:44
 1:32:11
1:32:11
2026-02-17 21:38
 1:39:31
1:39:31
2026-02-16 01:07
 1:35:41
1:35:41
2026-02-25 19:41
 1:54:47
1:54:47
2026-02-11 21:47
 2:11:42
2:11:42
2026-01-23 18:43
 2:12:40
2:12:40
2026-01-23 18:44
 1:52:50
1:52:50
2026-02-04 10:11
 1:29:24
1:29:24
2026-02-06 18:40
 1:29:22
1:29:22
2026-01-26 14:34
0/0
2021-09-22 20:39
 7:15
7:15
2026-02-10 12:00
2021-09-22 22:29
 7:00
7:00
2025-06-01 11:15
 7:11
7:11
2026-01-20 10:00
 25:31
25:31
2022-04-01 14:30
2021-09-22 22:54
 21:08
21:08
2025-01-09 16:39
 7:42
7:42
2024-12-17 12:21
 1:05:30
1:05:30
2025-06-27 13:20
2021-09-22 23:09
 12:51
12:51
2024-11-27 16:39
 7:04
7:04
2026-01-12 15:05
 7:20
7:20
2025-05-03 12:34
 7:04
7:04
2022-03-29 15:20
 3:27
3:27
2024-12-07 11:00
 11:06
11:06
2022-04-01 15:56
 7:05
7:05
2025-12-30 20:49
 7:19
7:19
2026-02-06 10:00
 11:00
11:00
2022-04-01 17:59
0/0
Скачать популярное видео
Популярное видео
 2:17:36
2:17:36
2025-07-24 20:55
 4:01
4:01
2023-10-12 11:54
 2:50
2:50
2024-07-04 15:48
 2:08:21
2:08:21
2023-05-03 20:56
2025-01-13 14:00
 1:47:36
1:47:36
2025-12-25 17:49
2024-12-16 20:15
 2:11:07
2:11:07
2023-04-25 22:52
2025-01-24 05:04
 7:04
7:04
2018-07-11 11:26
2024-12-31 14:00
2022-03-11 11:17
2024-08-05 22:22
 2:53
2:53
2025-04-24 09:53
 3:09
3:09
2024-05-30 14:13
2025-04-11 14:51
2025-06-17 19:00
 1:44:11
1:44:11
2025-12-25 22:29
 1:49:38
1:49:38
2024-03-12 00:19
 59:17
59:17
2026-02-01 14:02
0/0

