
 8:49
8:49
2024-11-03 19:25

 27:23
27:23

 27:23
27:23
2024-01-04 16:59
 11:45
11:45

 11:45
11:45
2024-01-11 18:34

 6:23
6:23

 6:23
6:23
2024-12-13 04:15

 5:58
5:58

 5:58
5:58
2025-01-19 10:30

 2:52
2:52

 2:52
2:52
2023-12-19 21:11

 4:22
4:22

 4:22
4:22
2024-04-11 11:30
 6:25
6:25

 6:25
6:25
2024-01-20 08:13

 2:44
2:44

 2:44
2:44
2024-03-14 06:08

 3:36
3:36

 3:36
3:36
2023-11-29 15:47

 1:31
1:31

 1:31
1:31
2025-05-26 21:35

 18:09
18:09

 18:09
18:09
2021-02-12 14:30

 3:35
3:35

 3:35
3:35
2019-04-29 07:57

 0:58
0:58

 0:58
0:58
2023-08-27 17:42

 11:09
11:09

 11:09
11:09
2023-10-05 17:25

 2:47
2:47

 2:47
2:47
2023-11-21 04:32
 4:14
4:14
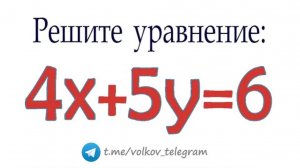
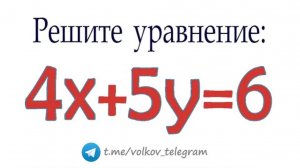 4:14
4:14
2023-07-29 13:01

 2:31
2:31
![Tural Everest, Руслан Добрый - Красивая (Премьера клипа 2025)]() 3:16
3:16
![Like Nastya – Fly Girl (Official Video 2025)]() 2:01
2:01
![Соня Белькевич - Подогналась (Премьера клипа 2025)]() 3:13
3:13
![KhaliF - Я розы тебе принес (Премьера клипа 2025)]() 2:06
2:06
![Владимир Ждамиров, Игорь Кибирев - Тик так (Премьера 2025)]() 3:30
3:30
![Эльдар Агачев - Путник (Премьера клипа 2025)]() 3:14
3:14
![Отабек Муминов - Кетябсан (Премьера клипа 2025)]() 3:17
3:17
![Маракеш, Сергей Наговицын - До свидания, кореша (Премьера клипа 2025)]() 3:20
3:20
![Леся Кир - Альфонс (Премьера клипа 2025)]() 3:23
3:23
![Enrasta - Франция (Премьера клипа 2025)]() 2:44
2:44
![Игорь Балан - Белая зима (Премьера 2025)]() 3:10
3:10
![Зульфия Чотчаева - Холодное сердце (Премьера клипа 2025)]() 2:52
2:52
![Алмас Багратиони - Дети света (Премьера клипа 2025)]() 2:52
2:52
![Карина Салагати - Сердце горца (Премьера клипа 2025)]() 3:18
3:18
![ZAMA - Глаза цвета кофе (Премьера клипа 2025)]() 2:57
2:57
![Даша Эпова - Мой любимый человек (Премьера клипа 2025)]() 2:11
2:11
![Ахрор Гуломов - Ёмгирлар (Премьера клипа 2025)]() 3:49
3:49
![Абрикоса, GOSHU - Удали из памяти (Премьера клипа 2025)]() 4:59
4:59
![Вика Ветер - Еще поживем (Премьера клипа 2025)]() 4:31
4:31
![Катя Маркеданец - Мама (Премьера клипа 2025)]() 3:32
3:32
![Крысы: Ведьмачья история | The Rats: A Witcher Tale (2025)]() 1:23:01
1:23:01
![Мужчина у меня в подвале | The Man in My Basement (2025)]() 1:54:48
1:54:48
![Безжалостная | Stone Cold Fox (2025)]() 1:25:31
1:25:31
![Только ты | All of You (2025)]() 1:38:22
1:38:22
![Святые из Бундока | The Boondock Saints (1999) (Гоблин)]() 1:48:30
1:48:30
![Большое смелое красивое путешествие | A Big Bold Beautiful Journey (2025)]() 1:49:20
1:49:20
![Протокол выхода | Exit Protocol (2025)]() 1:24:45
1:24:45
![Все дьяволы здесь | All the Devils are Here (2025)]() 1:31:39
1:31:39
![Большой куш / Спи#дили | Snatch (2000) (Гоблин)]() 1:42:50
1:42:50
![Не грози Южному Централу, попивая сок у себя в квартале | Don't Be a Menace to South Central (1995) (Гоблин)]() 1:28:57
1:28:57
![Свинтусы | The Twits (2025)]() 1:42:50
1:42:50
![Гедда | Hedda (2025)]() 1:48:23
1:48:23
![Чумовая пятница 2 | Freakier Friday (2025)]() 1:50:38
1:50:38
![Кей-поп-охотницы на демонов | KPop Demon Hunters (2025)]() 1:39:41
1:39:41
![Дом из динамита | A House of Dynamite (2025)]() 1:55:08
1:55:08
![Богомол | Samagwi (2025)]() 1:53:29
1:53:29
![Рука, качающая колыбель | The Hand That Rocks the Cradle (2025)]() 1:44:57
1:44:57
![Чёрный телефон 2 | Black Phone 2 (2025)]() 1:53:55
1:53:55
![Плохой Cанта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:28:32
1:28:32
![Трон: Арес | Tron: Ares (2025)]() 1:52:27
1:52:27
![Оранжевая корова]() 6:30
6:30
![Ну, погоди! Каникулы]() 7:09
7:09
![Команда Дино Сезон 2]() 12:31
12:31
![Лудлвилль]() 7:09
7:09
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Пакман в мире привидений]() 21:37
21:37
![Команда Дино. Исследователи Сезон 2]() 13:26
13:26
![Минифорс. Сила динозавров]() 12:51
12:51
![Чемпионы]() 7:12
7:12
![Приключения Пети и Волка]() 11:00
11:00
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Зомби Дамб]() 5:14
5:14
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Отважные мишки]() 13:00
13:00
![Синдбад и семь галактик Сезон 1]() 10:23
10:23
![Артур и дети круглого стола]() 11:22
11:22
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24
![Панда и петушок Лука]() 12:12
12:12
![Енотки]() 7:04
7:04

 2:31
2:31Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 432x232 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:16
3:16
2025-11-12 12:12
 2:01
2:01
2025-11-10 13:14
 3:13
3:13
2025-11-14 11:41
 2:06
2:06
2025-11-11 18:00
 3:30
3:30
2025-11-13 11:12
 3:14
3:14
2025-11-12 12:52
 3:17
3:17
2025-11-15 12:47
 3:20
3:20
2025-11-11 00:28
 3:23
3:23
2025-11-19 11:51
 2:44
2:44
2025-11-20 21:37
 3:10
3:10
2025-11-07 14:48
 2:52
2:52
2025-11-18 11:48
 2:52
2:52
2025-11-20 13:43
 3:18
3:18
2025-11-19 11:48
 2:57
2:57
2025-11-13 11:03
 2:11
2:11
2025-11-15 12:28
 3:49
3:49
2025-11-15 12:54
 4:59
4:59
2025-11-15 12:21
 4:31
4:31
2025-11-11 12:26
 3:32
3:32
2025-11-17 14:20
0/0
 1:23:01
1:23:01
2025-11-05 19:47
 1:54:48
1:54:48
2025-10-01 15:17
 1:25:31
1:25:31
2025-11-10 21:11
 1:38:22
1:38:22
2025-10-01 12:16
 1:48:30
1:48:30
2025-09-23 22:53
 1:49:20
1:49:20
2025-10-21 22:50
 1:24:45
1:24:45
2025-11-13 23:26
 1:31:39
1:31:39
2025-10-02 20:46
 1:42:50
1:42:50
2025-09-23 22:53
 1:28:57
1:28:57
2025-09-23 22:52
 1:42:50
1:42:50
2025-10-21 16:19
 1:48:23
1:48:23
2025-11-05 19:47
 1:50:38
1:50:38
2025-10-16 16:08
 1:39:41
1:39:41
2025-10-29 16:30
 1:55:08
1:55:08
2025-10-29 16:30
 1:53:29
1:53:29
2025-10-01 12:06
 1:44:57
1:44:57
2025-10-29 16:30
 1:53:55
1:53:55
2025-11-05 19:47
 1:28:32
1:28:32
2025-10-07 09:27
 1:52:27
1:52:27
2025-11-06 18:12
0/0
 6:30
6:30
2022-03-31 18:49
 7:09
7:09
2025-08-19 17:20
2021-09-22 22:40
 7:09
7:09
2023-07-06 19:20
2021-09-22 21:49
 21:37
21:37
2024-11-28 17:35
2021-09-22 22:54
 12:51
12:51
2024-11-27 16:39
 7:12
7:12
2025-11-21 03:26
 11:00
11:00
2022-04-01 17:59
2021-09-22 20:39
2021-09-22 21:03
 5:14
5:14
2024-11-28 13:12
 4:33
4:33
2024-12-17 16:56
 13:00
13:00
2024-11-29 13:39
2021-09-22 23:09
 11:22
11:22
2023-05-11 14:51
 12:24
12:24
2024-11-27 13:24
 12:12
12:12
2024-11-29 14:21
 7:04
7:04
2022-03-29 18:22
0/0

