
 12:36
12:36
2023-03-16 19:43

 11:29
11:29

 11:29
11:29
2023-09-06 13:27
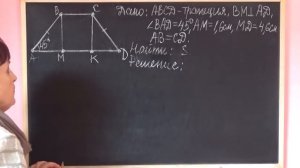
 21:00
21:00

 21:00
21:00
2023-09-11 09:16

 6:08
6:08

 6:08
6:08
2023-10-01 00:53

 4:57
4:57

 4:57
4:57
2025-03-28 11:12

 5:00
5:00

 5:00
5:00
2025-02-03 16:45

 6:56
6:56

 6:56
6:56
2024-11-15 05:30

 5:16
5:16

 5:16
5:16
2024-10-25 03:47

 39:17
39:17

 39:17
39:17
2024-08-18 07:57

 8:51
8:51

 8:51
8:51
2020-09-22 12:04

 42:23
42:23

 42:23
42:23
2024-08-06 14:03

 24:50
24:50

 24:50
24:50
2021-12-30 12:57

 36:56
36:56

 36:56
36:56
2024-08-18 07:55

 4:44
4:44
![Антон и Альфия - Январская вьюга (Премьера клипа 2026)]() 3:32
3:32
![Рустам Батербиев - Стерва-ночь (Премьера клипа 2026)]() 2:24
2:24
![Эльчин Кулиев - Сладкие сказки (Премьера клипа 2026)]() 4:08
4:08
![Самир Санаев - Дилрабо (Премьера клипа 2026)]() 4:17
4:17
![Ramon, Вагаршак Асриян - Кавказский бит (Премьера клипа 2026)]() 2:03
2:03
![Tural Everest, Руслан Добрый - Не хочу (Премьера клипа 2026)]() 2:46
2:46
![Сарвар Мадримов - Бора-бора (Премьера клипа 2026)]() 3:09
3:09
![KhaliF - Сияй (Премьера клипа 2026)]() 2:22
2:22
![Самира Сариева - Хоп-хоп (Премьера клипа 2026)]() 3:20
3:20
![Syuzi Dzhaginian - Сегодня я плачу (Премьера клипа 2026)]() 2:57
2:57
![ANIVAR - Маски (Премьера клипа 2026)]() 2:13
2:13
![Ирина Круг и Вика Ветер - Крестик (Премьера клипа 2026)]() 3:53
3:53
![Азамат Пхешхов, Руслан Шанов - Родная (Премьера клипа 2026)]() 3:25
3:25
![Оксана Ковалевская - Ты меня не ищи (Премьера клипа 2026)]() 3:05
3:05
![Ислам Итляшев - Боинг (Премьера клипа 2026)]() 2:42
2:42
![БАХТАВАР - В белом платье (Премьера клипа 2026)]() 3:17
3:17
![Артур Халатов - Красивая любовь (Премьера клипа 2026)]() 3:23
3:23
![Ислам Мальсуйгенов - Ледяное сердце (Премьера клипа 2026)]() 2:30
2:30
![Илёс Юнусий - Менга ургатманг сиз кандай яшашни (Премьера клипа 2026)]() 3:43
3:43
![Андрей Храмов - Я приглашу тебя на танец (Премьера клипа 2026)]() 4:01
4:01
![Один дома 2: Затерянный в Нью-Йорке | Home Alone 2: Lost in New York (1992)]() 2:00:06
2:00:06
![Безжалостная | Stone Cold Fox (2025)]() 1:25:31
1:25:31
![Пять ночей с Фредди 2 | Five Nights at Freddy's 2 (2025)]() 1:44:11
1:44:11
![Гарри Поттер и Кубок огня | Harry Potter and the Goblet of Fire (2005)]() 2:37:09
2:37:09
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Гарри Поттер и Дары Смерти: Часть II | Harry Potter and the Deathly Hallows - Part 2 (2011)]() 2:10:30
2:10:30
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Paзpушитeль миpoв | Worldbreaker (2025)]() 1:34:45
1:34:45
![Супергеройское кино | Superhero Movie (2008)]() 1:22:33
1:22:33
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Игры Биста. 2 сезон, 4 серия | Beast Games 2 season]() 1:01:10
1:01:10
![Астронавт | The Astronaut (2025)]() 1:30:31
1:30:31
![Семейный план 2 | The Family Plan 2 (2025)]() 1:46:14
1:46:14
![Боже. Как. Смешно. | Oh. What. Fun. (2025)]() 1:47:58
1:47:58
![Гарри Поттер и Дары Смерти: Часть I | Harry Potter and the Deathly Hallows - Part 1 (2010)]() 2:26:10
2:26:10
![Гарри Поттер и Тайная комната | Harry Potter and the Chamber of Secrets (2002)]() 2:54:28
2:54:28
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Гарри Поттер и Принц-полукровка | Harry Potter and the Half-Blood Prince (2009)]() 2:33:36
2:33:36
![Отпуск на двоих | People We Meet on Vacation (2026)]() 1:57:55
1:57:55
![Бугония | Bugonia (2025)]() 1:59:12
1:59:12
![Агент 203]() 21:08
21:08
![Хвостатые песенки]() 7:00
7:00
![Панда и Антилопа]() 12:08
12:08
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Сборники «Приключения Пети и Волка»]() 1:17:53
1:17:53
![Отважные мишки]() 13:00
13:00
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:46
10:46
![Приключения Пети и Волка]() 11:00
11:00
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Мартышкины]() 7:10
7:10
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![МиниФорс Сезон 1]() 13:12
13:12
![Зебра в клеточку]() 6:30
6:30
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Папа Супергерой Сезон 1]() 4:28
4:28
![Пип и Альба Сезон 1]() 11:02
11:02
![Сборники «Умка»]() 3:09:60
3:09:60
![МегаМен: Полный заряд Сезон 1]() 10:42
10:42
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Мультфильмы военных лет | Специальный проект к 80-летию Победы]() 7:20
7:20

 4:44
4:44Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 432x232 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:32
3:32
2026-01-28 09:47
 2:24
2:24
2026-01-15 13:21
 4:08
4:08
2026-01-15 10:48
 4:17
4:17
2026-01-28 12:17
 2:03
2:03
2026-01-20 10:47
 2:46
2:46
2026-01-28 12:09
 3:09
3:09
2026-01-14 15:26
 2:22
2:22
2026-01-22 11:38
 3:20
3:20
2026-01-28 10:04
 2:57
2:57
2026-01-28 11:50
 2:13
2:13
2026-01-10 14:36
 3:53
3:53
2026-01-23 18:04
 3:25
3:25
2026-01-23 19:30
 3:05
3:05
2026-01-24 13:42
 2:42
2:42
2026-01-20 01:15
 3:17
3:17
2026-01-28 09:57
 3:23
3:23
2026-01-23 17:57
 2:30
2:30
2026-01-24 13:36
 3:43
3:43
2026-01-22 10:47
 4:01
4:01
2026-01-15 13:30
0/0
 2:00:06
2:00:06
2025-12-25 15:39
 1:25:31
1:25:31
2025-11-10 21:11
 1:44:11
1:44:11
2025-12-25 22:29
 2:37:09
2:37:09
2025-12-25 15:40
 1:46:45
1:46:45
2026-01-19 12:39
 2:10:30
2:10:30
2025-12-25 15:40
 1:18:55
1:18:55
2025-11-21 14:16
 1:34:45
1:34:45
2025-11-27 19:40
 1:22:33
1:22:33
2025-11-21 14:16
 1:47:36
1:47:36
2025-12-25 17:49
 1:01:10
1:01:10
2026-01-15 03:46
 1:30:31
1:30:31
2026-01-14 15:48
 1:46:14
1:46:14
2025-11-26 06:44
 1:47:58
1:47:58
2025-12-09 13:32
 2:26:10
2:26:10
2025-12-25 15:40
 2:54:28
2:54:28
2025-12-25 15:41
 2:32:29
2:32:29
2025-11-17 11:22
 2:33:36
2:33:36
2025-12-25 15:40
 1:57:55
1:57:55
2026-01-14 15:48
 1:59:12
1:59:12
2025-11-29 02:45
0/0
 21:08
21:08
2025-01-09 16:39
 7:00
7:00
2025-06-01 11:15
 12:08
12:08
2025-06-10 14:59
2021-09-22 21:03
 1:17:53
1:17:53
2025-12-19 23:55
 13:00
13:00
2024-11-29 13:39
 10:46
10:46
2022-06-07 11:02
 11:00
11:00
2022-04-01 17:59
2021-09-22 23:36
 7:10
7:10
2025-12-30 18:33
 6:30
6:30
2018-04-03 10:35
2021-09-23 00:15
 6:30
6:30
2022-03-31 13:09
2021-09-22 21:49
2021-09-22 21:52
2021-09-22 23:37
 3:09:60
3:09:60
2025-12-11 18:53
2021-09-22 21:43
 3:28
3:28
2025-01-09 17:01
 7:20
7:20
2025-05-03 12:34
0/0

