
 2:09
2:09
2024-10-17 17:53

 5:49
5:49

 5:49
5:49
2023-12-01 10:19

 4:22
4:22

 4:22
4:22
2025-02-03 16:15

 2:19
2:19

 2:19
2:19
2024-10-25 03:02

 2:57:21
2:57:21

 2:57:21
2:57:21
2026-01-27 19:00
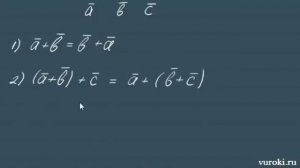
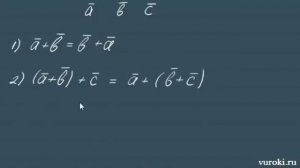 4:46
4:46
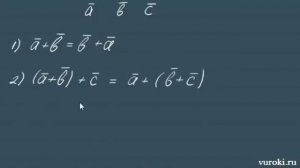
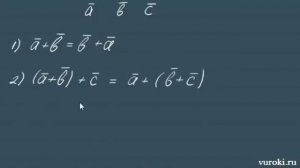 4:46
4:46
2023-09-27 12:44

 6:40
6:40

 6:40
6:40
2023-12-01 10:19
![Сложение и вычитание векторов]() 5:08
5:08
 5:08
5:08
2021-03-19 17:52
![Сумма нескольких векторов]() 3:44
3:44
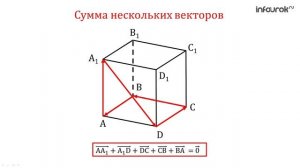 3:44
3:44
2021-03-19 17:52

 10:25
10:25

 10:25
10:25
2020-10-05 09:29
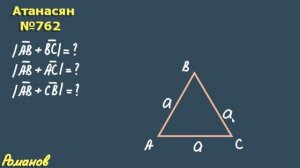
 6:51
6:51

 6:51
6:51
2023-09-24 04:18

 2:00:06
2:00:06

 2:00:06
2:00:06
2026-01-26 21:00

 10:25:31
10:25:31

 10:25:31
10:25:31
2025-05-02 07:58

 11:56:60
11:56:60

 11:56:60
11:56:60
2025-08-29 07:40

 1:14:36
1:14:36

 1:14:36
1:14:36
2026-01-26 11:58

 5:36
5:36

 5:36
5:36
2026-01-15 01:44

 11:59:14
11:59:14

 11:59:14
11:59:14
2025-12-11 08:06

 1:53:18
1:53:18
![Григорий Герасимов - Я другой (Премьера клипа 2026)]() 3:32
3:32
![DJ Serzh - Она играла лишь со мной (Премьера клипа 2026)]() 4:12
4:12
![Dabro - Зима, зима (Премьера клипа 2026)]() 3:17
3:17
![Восточный Округ - Когда ты за рулём (Премьера клипа 2026)]() 4:01
4:01
![Tural Everest - Забыла (Премьера клипа 2026)]() 2:44
2:44
![Бекзод Жахон - Бухоро (Премьера клипа 2026)]() 4:44
4:44
![Sasha Komovich - Расскажи, Снегурочка (Премьера клипа 2025)]() 2:13
2:13
![Как на Новый год в селе девочки гуляли]() 4:58
4:58
![Амина Магомедова - Танцуй со мной (Премьера клипа 2026)]() 3:08
3:08
![Толиб Тухтасинов & Гулинур - Гулихоним (Премьера клипа 2025)]() 3:12
3:12
![DJ Прозрачный - Новый год (Премьера клипа 2025)]() 3:17
3:17
![Оксана Ковалевская - Ты меня не ищи (Премьера клипа 2026)]() 3:05
3:05
![Ислам Мальсуйгенов - Ледяное сердце (Премьера клипа 2026)]() 2:30
2:30
![AY YOLA, ALSOU - Ay, bylbylym (Премьера клипа 2026)]() 4:08
4:08
![Рустам Батербиев - Стерва-ночь (Премьера клипа 2026)]() 2:24
2:24
![SOPRANO Турецкого & Кай Син - Ах мамочка, на саночках (Премьера клипа 2026)]() 3:40
3:40
![Наталья Влади, Любовь Рыбкина - В жизни успеть (Премьера клипа 2026)]() 2:37
2:37
![Zhamil Turan - Одна на миллион (Премьера клипа 2026)]() 2:57
2:57
![Азамат Пхешхов, Руслан Шанов - Родная (Премьера клипа 2026)]() 3:25
3:25
![Эльчин Кулиев - Сладкие сказки (Премьера клипа 2026)]() 4:08
4:08
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Сожалею о тебе | Regretting You (2025)]() 1:55:53
1:55:53
![Бегущий человек | The Running Man (2025)]() 2:16:29
2:16:29
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Один дома | Home Alone (1990)]() 1:43:02
1:43:02
![Мерв | Merv (2025)]() 1:46:56
1:46:56
![Ловчий смерти | Deathstalker (2025)]() 1:42:60
1:42:60
![Прощай Джун | Goodbye June (2025)]() 1:56:04
1:56:04
![Гарри Поттер и Дары Смерти: Часть II | Harry Potter and the Deathly Hallows - Part 2 (2011)]() 2:10:30
2:10:30
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Джей Келли | Jay Kelly (2025)]() 2:13:54
2:13:54
![Гарри Поттер и узник Азкабана | Harry Potter and the Prisoner of Azkaban (2004)]() 2:21:46
2:21:46
![Вальсируя с Брандо | Waltzing with Brando (2024)]() 1:44:15
1:44:15
![Игры Биста. 2 сезон, 5 серия | Beast Games 2 season]() 49:20
49:20
![Побег из плена | Prisoner of War (2025)]() 1:52:58
1:52:58
![Носферату | Nosferatu (2024)]() 2:12:40
2:12:40
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Безжалостная | Stone Cold Fox (2025)]() 1:25:31
1:25:31
![Астронавт | The Astronaut (2025)]() 1:30:31
1:30:31
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![Врумиз. 1 сезон]() 13:10
13:10
![Панда и петушок Лука]() 12:12
12:12
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Супер Дино]() 12:41
12:41
![Пластилинки]() 25:31
25:31
![Школьный автобус Гордон]() 12:34
12:34
![Сборники «Оранжевая корова»]() 1:05:01
1:05:01
![Оранжевая корова]() 6:30
6:30
![Богатырята]() 11:00
11:00
![Корги по имени Моко. Домашние животные]() 1:13
1:13
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Чемпионы]() 7:15
7:15
![Отряд А. Игрушки-спасатели]() 13:06
13:06
![Приключения Тайо]() 12:50
12:50
![Пакман в мире привидений]() 21:37
21:37
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32

 1:53:18
1:53:18Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 432x232 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:32
3:32
2026-01-14 15:22
 4:12
4:12
2026-01-12 10:16
 3:17
3:17
2026-01-23 19:44
 4:01
4:01
2026-01-16 16:46
 2:44
2:44
2026-01-23 18:15
 4:44
4:44
2026-01-04 12:06
 2:13
2:13
2026-01-01 11:00
 4:58
4:58
2026-01-01 11:35
 3:08
3:08
2026-01-15 13:41
 3:12
3:12
2026-01-01 11:23
 3:17
3:17
2025-12-31 13:58
 3:05
3:05
2026-01-24 13:42
 2:30
2:30
2026-01-24 13:36
 4:08
4:08
2026-01-07 22:29
 2:24
2:24
2026-01-15 13:21
 3:40
3:40
2026-01-20 10:50
 2:37
2:37
2026-01-22 10:58
 2:57
2:57
2026-01-14 15:11
 3:25
3:25
2026-01-23 19:30
 4:08
4:08
2026-01-15 10:48
0/0
 1:47:25
1:47:25
2025-11-27 03:58
 1:18:55
1:18:55
2025-11-21 14:16
 1:55:53
1:55:53
2025-12-17 23:52
 2:16:29
2:16:29
2025-12-17 23:52
 2:32:29
2:32:29
2025-11-17 11:22
 1:43:02
1:43:02
2025-12-25 15:40
 1:46:56
1:46:56
2025-12-12 13:56
 1:42:60
1:42:60
2025-12-03 17:17
 1:56:04
1:56:04
2026-01-21 16:22
 2:10:30
2:10:30
2025-12-25 15:40
 1:47:36
1:47:36
2025-12-25 17:49
 2:13:54
2:13:54
2025-12-08 13:26
 2:21:46
2:21:46
2025-12-25 15:40
 1:44:15
1:44:15
2025-11-07 20:19
 49:20
49:20
2026-01-23 13:36
 1:52:58
1:52:58
2026-01-26 14:34
 2:12:40
2:12:40
2026-01-23 18:44
 1:46:45
1:46:45
2026-01-19 12:39
 1:25:31
1:25:31
2025-11-10 21:11
 1:30:31
1:30:31
2026-01-14 15:48
0/0
2021-09-22 22:45
2021-09-22 20:39
 6:30
6:30
2018-04-03 10:35
2021-09-24 16:00
 12:12
12:12
2024-11-29 14:21
2021-09-22 21:03
 12:41
12:41
2024-11-28 12:54
 25:31
25:31
2022-04-01 14:30
 12:34
12:34
2024-12-02 14:42
 1:05:01
1:05:01
2025-12-12 12:24
 6:30
6:30
2025-12-30 19:54
2026-01-12 13:08
 1:13
1:13
2024-11-29 14:40
2021-09-22 23:36
 7:15
7:15
2025-12-10 10:00
 13:06
13:06
2024-11-28 16:30
 12:50
12:50
2024-12-17 13:25
 21:37
21:37
2024-11-28 17:35
 13:00
13:00
2024-11-28 16:19
2021-09-22 21:49
0/0

