
 4:56
4:56
2025-01-05 10:01

 2:39
2:39

 2:39
2:39
2025-04-09 06:22

 2:41
2:41

 2:41
2:41
2025-01-05 09:00
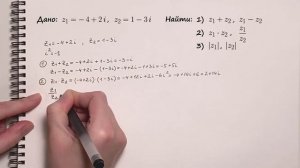
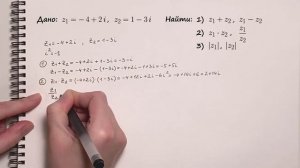 7:24
7:24
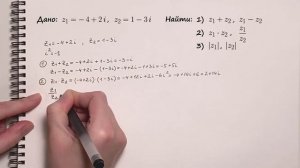
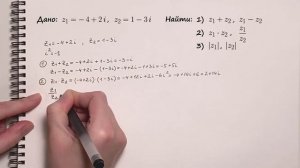 7:24
7:24
2023-09-26 04:48

 2:57:56
2:57:56

 2:57:56
2:57:56
2026-01-21 17:00

 21:31
21:31

 21:31
21:31
2019-10-22 21:46

 5:19
5:19

 5:19
5:19
2023-09-10 14:40
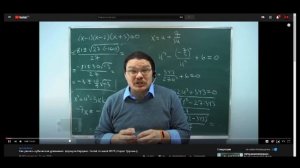
 7:01
7:01

 7:01
7:01
2023-09-19 16:26

 10:08
10:08

 10:08
10:08
2024-09-16 16:08

 9:10
9:10

 9:10
9:10
2022-04-08 00:03

 5:23
5:23

 5:23
5:23
2024-07-26 16:29

 10:08
10:08

 10:08
10:08
2024-07-26 16:17

 6:09
6:09

 6:09
6:09
2023-12-03 01:30

 2:00:06
2:00:06

 2:00:06
2:00:06
2026-01-26 21:00

 10:25:31
10:25:31

 10:25:31
10:25:31
2025-05-02 07:58

 2:32:19
2:32:19

 2:32:19
2:32:19
2023-09-10 18:25

 1:35:38
1:35:38

 1:35:38
1:35:38
2026-01-30 10:57

 5:36
5:36
![БАХТАВАР - В белом платье (Премьера клипа 2026)]() 3:17
3:17
![Артур Бесаев - Там где горы (Премьера клипа 2026)]() 2:15
2:15
![Zhamil Turan - Одна на миллион (Премьера клипа 2026)]() 2:57
2:57
![Шавкат Зулфикор - Жигарлар (Премьера клипа 2026)]() 5:53
5:53
![Tural Everest, Руслан Добрый - Не хочу (Премьера клипа 2026)]() 2:46
2:46
![Cvetocek7 - Молния (Премьера клипа 2026)]() 2:41
2:41
![DJ Serzh - Она играла лишь со мной (Премьера клипа 2026)]() 4:12
4:12
![Медина Мелик - Дура (Премьера клипа 2026)]() 2:41
2:41
![NAIMAN - Тебя украду (Премьера клипа 2026)]() 2:28
2:28
![Гунеша - Юр кетамиз (Премьера клипа 2026)]() 3:13
3:13
![Сарвар Мадримов - Бора-бора (Премьера клипа 2026)]() 3:09
3:09
![Jazzdauren - Юность (Премьера клипа 2026)]() 2:44
2:44
![Зироатхон - Бевафо (Премьера клипа 2026)]() 3:15
3:15
![SOPRANO Турецкого & Кай Син - Ах мамочка, на саночках (Премьера клипа 2026)]() 3:40
3:40
![Кравц - 99 проблем (Премьера клипа 2026)]() 2:30
2:30
![Рустам Нахушев - Живя по совести (Премьера клипа 2026)]() 3:40
3:40
![Дана Лахова - Ай, яй, яй (Премьера клипа 2026)]() 2:53
2:53
![Антон и Альфия - Январская вьюга (Премьера клипа 2026)]() 3:32
3:32
![Виктор Королёв - А ты яблоко ела (Премьера 2026)]() 3:44
3:44
![Арина Войт - Смелая (Премьера клипа 2026)]() 2:52
2:52
![Мелодия их мечты | Song Sung Blue (2025)]() 2:12:15
2:12:15
![Кристи | Christy (2025)]() 2:15:04
2:15:04
![Тихое место: День первый | A Quiet Place: Day One (2024)]() 1:39:30
1:39:30
![Мерв | Merv (2025)]() 1:46:56
1:46:56
![Игры Биста. 2 сезон, 2 серия | Beast Games 2 season]() 58:23
58:23
![Отпуск на двоих | People We Meet on Vacation (2026)]() 1:57:55
1:57:55
![Игры Биста. 2 сезон, 5 серия | Beast Games 2 season]() 49:20
49:20
![Астронавт | The Astronaut (2025)]() 1:30:31
1:30:31
![Давид | David (2025)]() 1:49:18
1:49:18
![Гарри Поттер и философский камень | Harry Potter and the Sorcerer's Stone (2001)]() 2:32:26
2:32:26
![Гарри Поттер и Дары Смерти: Часть I | Harry Potter and the Deathly Hallows - Part 1 (2010)]() 2:26:10
2:26:10
![Голубая луна | Blue Moon (2025)]() 1:40:33
1:40:33
![Гарри Поттер и Кубок огня | Harry Potter and the Goblet of Fire (2005)]() 2:37:09
2:37:09
![Гарри Поттер и Орден Феникса | Harry Potter and the Order of the Phoenix (2007)]() 2:18:19
2:18:19
![Один дома 2: Затерянный в Нью-Йорке | Home Alone 2: Lost in New York (1992)]() 2:00:06
2:00:06
![Сожалею о тебе | Regretting You (2025)]() 1:55:53
1:55:53
![Злая. Часть 2 | Wicked: For Good (2025)]() 2:17:37
2:17:37
![Доверие | Trust (2025)]() 1:30:44
1:30:44
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Пять ночей с Фредди 2 | Five Nights at Freddy's 2 (2025)]() 1:44:11
1:44:11
![Агент 203]() 21:08
21:08
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Богатырята]() 11:00
11:00
![Тайны Медовой долины]() 7:01
7:01
![Панда и Антилопа]() 12:08
12:08
![Псэмми. Пять детей и волшебство Сезон 1]() 12:17
12:17
![Зебра в клеточку]() 6:30
6:30
![МиниФорс Сезон 1]() 13:12
13:12
![Команда Дино. Исследователи Сезон 2]() 13:26
13:26
![Мартышкины]() 7:10
7:10
![Пип и Альба Сезон 1]() 11:02
11:02
![МегаМен: Полный заряд Сезон 1]() 10:42
10:42
![Простоквашино]() 6:44
6:44
![Мотофайтеры]() 13:10
13:10
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Хвостатые песенки]() 7:00
7:00
![Енотки]() 7:08
7:08
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Шахерезада. Нерассказанные истории Сезон 1]() 23:53
23:53
![Истории Баданаму Сезон 1]() 10:02
10:02

 5:36
5:36Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:17
3:17
2026-01-28 09:57
 2:15
2:15
2026-01-16 16:50
 2:57
2:57
2026-01-14 15:11
 5:53
5:53
2026-01-10 14:39
 2:46
2:46
2026-01-28 12:09
 2:41
2:41
2026-01-16 16:41
 4:12
4:12
2026-01-12 10:16
 2:41
2:41
2026-01-13 10:54
 2:28
2:28
2026-01-28 12:37
 3:13
3:13
2026-01-12 10:24
 3:09
3:09
2026-01-14 15:26
 2:44
2:44
2026-01-28 11:45
 3:15
3:15
2026-01-28 12:20
 3:40
3:40
2026-01-20 10:50
 2:30
2:30
2026-01-14 15:04
 3:40
3:40
2026-01-23 14:27
 2:53
2:53
2026-01-22 11:17
 3:32
3:32
2026-01-28 09:47
 3:44
3:44
2026-01-08 12:44
 2:52
2:52
2026-01-08 12:25
0/0
 2:12:15
2:12:15
2026-01-21 16:23
 2:15:04
2:15:04
2025-12-12 14:01
 1:39:30
1:39:30
2026-01-23 18:43
 1:46:56
1:46:56
2025-12-12 13:56
 58:23
58:23
2026-01-07 23:52
 1:57:55
1:57:55
2026-01-14 15:48
 49:20
49:20
2026-01-23 13:36
 1:30:31
1:30:31
2026-01-14 15:48
 1:49:18
1:49:18
2026-01-29 11:25
 2:32:26
2:32:26
2025-12-25 15:41
 2:26:10
2:26:10
2025-12-25 15:40
 1:40:33
1:40:33
2025-12-17 23:52
 2:37:09
2:37:09
2025-12-25 15:40
 2:18:19
2:18:19
2025-12-25 15:40
 2:00:06
2:00:06
2025-12-25 15:39
 1:55:53
1:55:53
2025-12-17 23:52
 2:17:37
2:17:37
2026-01-14 15:48
 1:30:44
1:30:44
2025-12-17 23:52
 1:46:45
1:46:45
2026-01-19 12:39
 1:44:11
1:44:11
2025-12-25 22:29
0/0
 21:08
21:08
2025-01-09 16:39
2021-09-22 23:36
2026-01-12 13:08
 7:01
7:01
2022-03-30 17:25
 12:08
12:08
2025-06-10 14:59
2021-09-22 22:23
 6:30
6:30
2022-03-31 13:09
2021-09-23 00:15
2021-09-22 22:54
 7:10
7:10
2025-12-30 18:33
2021-09-22 23:37
2021-09-22 21:43
 6:44
6:44
2026-01-12 16:22
 13:10
13:10
2024-11-27 14:57
 4:33
4:33
2024-12-17 16:56
 7:00
7:00
2025-06-01 11:15
 7:08
7:08
2025-12-30 21:34
2021-09-22 20:39
2021-09-22 23:25
2021-09-22 21:29
0/0

