
 3:30
3:30
2025-01-05 10:15

 7:51
7:51

 7:51
7:51
2023-11-27 13:50

 4:43
4:43

 4:43
4:43
2024-04-17 12:49

 2:01
2:01

 2:01
2:01
2025-04-10 13:57

 5:15
5:15

 5:15
5:15
2024-02-13 02:34

 3:44
3:44

 3:44
3:44
2025-02-16 15:12

 10:46
10:46

 10:46
10:46
2023-12-03 18:53

 13:06
13:06

 13:06
13:06
2025-01-05 08:00

 4:36
4:36

 4:36
4:36
2024-12-29 11:15

 52:45
52:45

 52:45
52:45
2023-12-03 21:16

 3:20
3:20

 3:20
3:20
2023-12-19 23:06
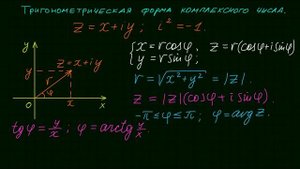
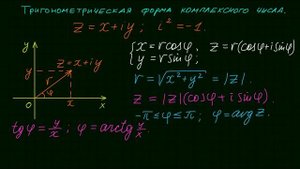 14:40
14:40
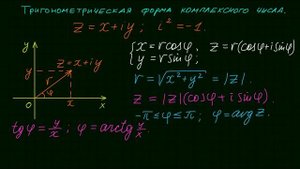
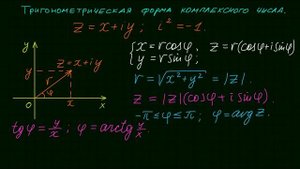 14:40
14:40
2023-09-25 19:55
 7:01
7:01

 7:01
7:01
2023-09-19 16:26
 7:24
7:24
 7:24
7:24
2023-09-26 04:48

 10:42
10:42

 10:42
10:42
2023-09-24 00:24

 8:42
8:42

 8:42
8:42
2023-09-11 20:06

 7:29
7:29

 7:29
7:29
2024-03-31 04:49

 4:59
4:59
![Азимжон Сайфуллаев - Тупрок буламиз (Премьера клипа 2025)]() 4:38
4:38
![Аля Вайш - По кругу (Премьера клипа 2025)]() 2:37
2:37
![Артур Халатов - Девочка моя (Премьера клипа 2025)]() 2:37
2:37
![ИЮЛА - Ты был прав (Премьера клипа 2025)]() 2:21
2:21
![MEDNA - Алё (Премьера клипа 2025)]() 2:28
2:28
![Фаррух Хамраев - Отажоним булсайди (Премьера клипа 2025)]() 3:08
3:08
![Рейсан Магомедкеримов, Ренат Омаров - Бла-та-та (Премьера клипа 2025)]() 2:26
2:26
![INSTASAMKA - BOSS (Премьера клипа 2025)]() 3:41
3:41
![Руслан Гасанов, Роман Ткаченко - Друзьям (Премьера клипа 2025)]() 3:20
3:20
![Зафар Эргашов - Мусофирда каридим (Премьера клипа 2025)]() 4:58
4:58
![Дана Лахова - Одинокая луна (Премьера клипа 2025)]() 2:15
2:15
![KhaliF - Где бы не был я (Премьера клипа 2025)]() 2:53
2:53
![Светлана Ларионова - Осень отстой (Премьера клипа 2025)]() 3:30
3:30
![Anette - Erjanik em (Official Video 2025)]() 3:36
3:36
![Рустам Нахушев, Зульфия Чотчаева - Каюсь (Премьера клипа 2025)]() 3:20
3:20
![ARTIX - Ай, джана-джана (Премьера клипа 2025)]() 2:24
2:24
![Алибек Казаров - Чужая жена (Премьера клипа 2025)]() 2:37
2:37
![Бонухон & Сардорбек Машарипов - Шанс (Премьера клипа 2025)]() 3:28
3:28
![SERYABKINA, Брутто - Светофоры (Премьера клипа 2025)]() 3:49
3:49
![Азиз Абдуллох - Аллохнинг айтгани булади (Премьера клипа 2025)]() 3:40
3:40
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![Мальчишник в Таиланде | Changeland (2019)]() 1:25:47
1:25:47
![Лучшее Рождество! | Nativity! (2009)]() 1:46:00
1:46:00
![Псы войны | Hounds of War (2024)]() 1:34:38
1:34:38
![Плохие парни 2 | The Bad Guys 2 (2025)]() 1:43:51
1:43:51
![Четверо похорон и одна свадьба | Plots with a View (2002)]() 1:32:52
1:32:52
![Чумовая пятница 2 | Freakier Friday (2025)]() 1:50:38
1:50:38
![Эффект бабочки | The Butterfly Effect (2003)]() 1:53:35
1:53:35
![Диспетчер | Relay (2025)]() 1:51:56
1:51:56
![Непрощённая | The Unforgivable (2021)]() 1:54:10
1:54:10
![Тот самый | Him (2025)]() 1:36:20
1:36:20
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Храброе сердце | Braveheart (1995)]() 2:57:46
2:57:46
![Свинья | Pig (2021)]() 1:31:23
1:31:23
![Счастливчик Гилмор 2 | Happy Gilmore (2025)]() 1:57:36
1:57:36
![F1 (2025)]() 2:35:53
2:35:53
![Супруги Роуз | The Roses (2025)]() 1:45:29
1:45:29
![Дом из динамита | A House of Dynamite (2025)]() 1:55:08
1:55:08
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Таинственные золотые города]() 23:04
23:04
![Новогодние мультики – Союзмультфильм]() 7:04
7:04
![Панда и петушок Лука]() 12:12
12:12
![Простоквашино. Финансовая грамотность]() 3:27
3:27
![Сборники «Простоквашино»]() 1:04:60
1:04:60
![Врумиз. 1 сезон]() 13:10
13:10
![Шахерезада. Нерассказанные истории Сезон 1]() 23:53
23:53
![Команда Дино. Исследователи Сезон 2]() 13:26
13:26
![Кадеты Баданаму Сезон 1]() 11:50
11:50
![Последний книжный магазин]() 11:20
11:20
![Супер Зак]() 11:38
11:38
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:21
10:21
![МегаМен: Полный заряд Сезон 1]() 10:42
10:42
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![Отважные мишки]() 13:00
13:00
![Енотки]() 7:04
7:04
![Приключения Тайо]() 12:50
12:50
![Чемпионы]() 7:21
7:21
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Минифорс. Сила динозавров]() 12:51
12:51

 4:59
4:59Скачать видео
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 4:38
4:38
2025-10-23 11:27
 2:37
2:37
2025-10-23 11:33
 2:37
2:37
2025-10-28 10:22
 2:21
2:21
2025-10-18 10:16
 2:28
2:28
2025-10-21 09:22
 3:08
3:08
2025-10-18 10:28
 2:26
2:26
2025-10-22 14:10
 3:41
3:41
2025-10-23 13:04
 3:20
3:20
2025-10-25 12:59
 4:58
4:58
2025-10-18 10:31
 2:15
2:15
2025-10-22 14:16
 2:53
2:53
2025-10-28 12:16
 3:30
3:30
2025-10-24 11:42
 3:36
3:36
2025-10-18 10:11
 3:20
3:20
2025-10-30 10:39
 2:24
2:24
2025-10-28 12:09
 2:37
2:37
2025-10-30 10:49
 3:28
3:28
2025-10-24 11:20
 3:49
3:49
2025-10-25 12:52
 3:40
3:40
2025-10-18 10:34
0/0
 1:35:11
1:35:11
2025-10-13 12:06
 1:29:27
1:29:27
2025-09-07 22:44
 1:25:47
1:25:47
2025-08-27 17:17
 1:46:00
1:46:00
2025-08-27 17:17
 1:34:38
1:34:38
2025-08-28 15:32
 1:43:51
1:43:51
2025-08-26 16:18
 1:32:52
1:32:52
2025-08-15 19:31
 1:50:38
1:50:38
2025-10-16 16:08
 1:53:35
1:53:35
2025-09-11 08:20
 1:51:56
1:51:56
2025-09-24 11:35
 1:54:10
1:54:10
2025-08-27 17:17
 1:36:20
1:36:20
2025-10-09 20:02
 2:15:54
2:15:54
2025-10-13 19:02
 2:57:46
2:57:46
2025-08-31 01:03
 1:31:23
1:31:23
2025-08-27 18:01
 1:57:36
1:57:36
2025-08-21 17:43
 2:35:53
2:35:53
2025-08-26 11:45
 1:45:29
1:45:29
2025-10-23 18:26
 1:55:08
1:55:08
2025-10-29 16:30
 2:09:55
2:09:55
2025-10-05 00:32
0/0
 23:04
23:04
2025-01-09 17:26
 7:04
7:04
2023-07-25 00:09
 12:12
12:12
2024-11-29 14:21
 3:27
3:27
2024-12-07 11:00
 1:04:60
1:04:60
2025-09-02 13:47
2021-09-24 16:00
2021-09-22 23:25
2021-09-22 22:54
2021-09-22 21:17
 11:20
11:20
2025-09-12 10:05
2021-09-22 22:07
 10:21
10:21
2025-09-11 10:05
2021-09-22 21:43
 6:30
6:30
2018-04-03 10:35
 13:00
13:00
2024-11-29 13:39
 7:04
7:04
2022-03-29 18:22
 12:50
12:50
2024-12-17 13:25
 7:21
7:21
2025-10-07 09:00
2021-09-22 21:49
 12:51
12:51
2024-11-27 16:39
0/0

