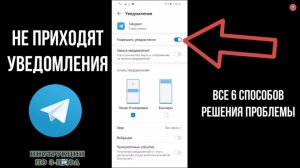
 3:45
3:45
2024-04-05 09:00

 1:37
1:37

 1:37
1:37
2025-03-03 12:07

 17:45
17:45

 17:45
17:45
2024-12-08 10:51
 2:09
2:09

 2:09
2:09
2024-05-01 14:55
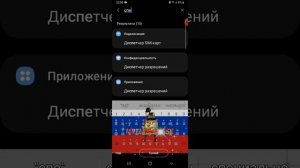
 1:02
1:02

 1:02
1:02
2023-12-07 15:01

 5:37
5:37

 5:37
5:37
2025-03-16 12:44

 4:28
4:28

 4:28
4:28
2025-02-14 13:45

 3:10
3:10

 3:10
3:10
2024-01-26 17:06

 4:02
4:02

 4:02
4:02
2024-09-30 11:33

 4:16
4:16

 4:16
4:16
2023-12-12 15:28

 2:08
2:08

 2:08
2:08
2025-05-28 10:14

 11:25
11:25

 11:25
11:25
2023-09-14 23:02

 34:38
34:38

 34:38
34:38
2021-06-23 20:16

 1:38
1:38

 1:38
1:38
2022-04-14 08:26

 17:12
17:12

 17:12
17:12
2025-05-10 09:05

 5:44
5:44

 5:44
5:44
2023-08-04 11:47

 2:14
2:14

 2:14
2:14
2023-09-15 20:57

 16:51
16:51
![Премьера Клипа! Егор Крид и Григорий Лепс - Пепел (OST "Вниз")]() 3:15
3:15
![Премьера клипа! Моя Мишель и Баста - Не поняла]() 3:22
3:22
![Премьера! 3-ий Январь и IL’GIZ - Дорога дальняя]() 2:44
2:44
![Премьера клипа! ANIVAR - ТАК И НЕ ПОНЯЛ]() 2:37
2:37
![Премьера клипа! Люся Чеботина - Каблук]() 3:15
3:15
![Премьера клипа! Стас Костюшкин и Настасья Самбурская - «Невеста»]() 2:37
2:37
![Премьера клипа! Мари aka Краймбрери — Интеллект]() 2:32
2:32
![Премьера клипа! GAYAZOV$ BROTHER$ – Выбираю море]() 3:12
3:12
![Премьера клипа! Артур Пирожков и Элвин Грей - Женщина-Магнит]() 3:13
3:13
![Премьера клипа! ДжаЯмми - Вива!]() 3:00
3:00
![Премьера клипа! ARTEE - А я так жду]() 3:23
3:23
![Премьера клипа! Моя Мишель - Иногда]() 3:12
3:12
![Премьера клипа! NECHAEV - Скучаю по тебе]() 2:49
2:49
![Премьера клипа! NEMIGA, NAVAI - Пойдем в кино]() 2:47
2:47
![Премьера! Ваня Дмитриенко и Аня Пересильд - Силуэт (OST «Алиса в Стране Чудес»)]() 2:47
2:47
![Премьера! 3-ий Январь и IL'GIZ - Дорога дальняя]() 2:44
2:44
![Премьера клипа! Анет Сай - Не трать время]() 3:15
3:15
![Премьера клипа! Мари Краймбрери – Сегодня мой лучший день]() 3:10
3:10
![Премьера клипа! Инна Вальтер - С козырей зашёл]() 3:31
3:31
![Премьера клипа! 55x55 – СВЭГ (feat. Ксения Собчак)]() 1:42
1:42
![Последний клиент]() 1:33:23
1:33:23
![Скелеты Железного острова]() 1:25:19
1:25:19
![Терминатор 2: Судный день | Terminator 2: Judgment Day (1991) (Гоблин)]() 2:36:13
2:36:13
![Война между людьми и ИИ. Серия 12]() 21:08
21:08
![Война между людьми и ИИ. Серия 9]() 18:53
18:53
![Посредники]() 2:04:01
2:04:01
![Война между людьми и ИИ. Серия 6]() 20:46
20:46
![Легенды: Гробница дракона (2013)]() 1:32:30
1:32:30
![Порочный круг (2025)]() 1:43:41
1:43:41
![Порочный круг | Vicious (2025)]() 1:42:30
1:42:30
![Война между людьми и ИИ. Серия 8]() 19:19
19:19
![102 далматинца (фильм, 2000) | 101 далматинец 2 часть]() 2:08:47
2:08:47
![Война между людьми и ИИ. Серия 2]() 19:38
19:38
![Терминатор | The Terminator (1984) (Гоблин)]() 1:47:17
1:47:17
![101 далматинец (фильм, 1996) | Круэлла и далматинцы]() 2:12:42
2:12:42
![Аббатство Даунтон 3 (2025)]() 2:03:57
2:03:57
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Облако (2024)]() 2:04:02
2:04:02
![Комната (2003)]() 1:39:52
1:39:52
![Сирены (2025) Netflix]() 4:26:06
4:26:06
![Гномео и Джульетта (2011) / Gnomeo & Juliet]()
 1:23:51
1:23:51
![Странные чары (2015) / Strange Magic]()
 1:39:20
1:39:20
![Барби: Скиппер и большое приключение с детьми (2023) / Skipper and the Big Babysitting Adventure]()
 1:02:58
1:02:58
![Земля до начала времён 12: Великий День птиц (2006) / The Land Before Time XII]()
 1:20:30
1:20:30
![Волшебный парк Джун (2019) / Wonder Park]()
 1:25:17
1:25:17
![Упс… Ной уплыл! (2015) / Ooops! Noah Is Gone...]()
 1:26:28
1:26:28
![Земля до начала времён 4: Путешествие в Землю Туманов (1996) / The Land Before Time IV]()
 1:13:52
1:13:52
![Земля до начала времён 11: Вторжение Мышезавров (2005) / The Land Before Time XI]()
 1:20:52
1:20:52
![Земля до начала времён 5: Таинственный остров (1997) / The Land Before Time V]()
 1:13:30
1:13:30
![Приключения Десперо (2008) / The Tale of Despereaux]()
 1:33:38
1:33:38
![Земля до начала времён 3: В поисках воды (1995) / The Land Before Time III]()
 1:10:48
1:10:48
![Земля до начала времён 7: Камень Холодного Огня (2000) / The Land Before Time VII]()
 1:14:10
1:14:10
![Плохие парни: Жутковатое ограбление (2024) / The Bad Guys: Haunted Heist]()
 22:03
22:03
![Альфа и Омега 5: Семейные каникулы (2014) / Alpha and Omega: Family Vacation]()
 43:30
43:30
![Барби: Виртуальный мир (2017) / Barbie Video Game Hero]()
 1:12:19
1:12:19
![Девочки из Эквестрии. Пропуск за кулисы для Сансет (2018) / Equestria Girls. Sunset's Backstage Pass]()
 44:08
44:08
![Плохие парни: Очень плохой праздник (2023) / The Bad Guys: A Very Bad Holiday]()
 22:30
22:30
![Науэль и волшебная книга (2020) / Nauel and the Magic Book]()
 1:37:06
1:37:06
![Земля до начала времён 8: Великая стужа (2001) / The Land Before Time VIII]()
 1:15:49
1:15:49
![Эти прекрасные мультяшки: Рождественский выпуск (1992) / It's a Wonderful Christmas Special]()
 22:22
22:22

 16:51
16:51Скачать видео
| 426x240 | ||
| 640x360 | ||
| 854x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:15
3:15
2025-08-29 15:48
 3:22
3:22
2025-08-27 12:34
 2:44
2:44
2025-09-13 14:31
 2:37
2:37
2025-09-07 15:55
 3:15
3:15
2025-09-17 21:08
 2:37
2:37
2025-09-02 11:35
 2:32
2:32
2025-08-14 17:53
 3:12
3:12
2025-08-10 17:27
 3:13
3:13
2025-09-19 18:07
 3:00
3:00
2025-08-15 12:03
 3:23
3:23
2025-08-23 11:31
2025-10-08 20:01
 2:49
2:49
2025-10-03 12:00
 2:47
2:47
2025-10-10 09:59
 2:47
2:47
2025-10-10 09:59
 2:44
2:44
2025-08-26 15:20
 3:15
3:15
2025-09-02 11:36
 3:10
3:10
2025-09-26 10:45
2025-09-30 09:56
2025-09-28 15:10
0/0
 1:33:23
1:33:23
2025-10-13 11:36
 1:25:19
1:25:19
2025-10-13 11:18
 2:36:13
2:36:13
2025-10-07 09:27
2025-10-15 10:26
2025-10-15 10:25
 2:04:01
2:04:01
2025-10-13 11:37
2025-10-15 10:25
2025-10-10 08:28
 1:43:41
1:43:41
2025-10-13 12:39
 1:42:30
1:42:30
2025-10-14 20:27
2025-10-15 10:25
 2:08:47
2:08:47
2025-10-14 17:39
2025-10-15 10:24
 1:47:17
1:47:17
2025-10-07 09:28
 2:12:42
2:12:42
2025-10-14 17:28
 2:03:57
2:03:57
2025-10-05 21:44
 1:35:11
1:35:11
2025-10-13 12:06
 2:04:02
2:04:02
2025-10-12 13:06
 1:39:52
1:39:52
2025-10-08 18:11
 4:26:06
4:26:06
2025-10-12 20:27
0/0

 1:23:51
1:23:51
2025-09-10 18:00

 1:39:20
1:39:20
2025-10-13 18:00

 1:02:58
1:02:58
2025-09-07 18:00

 1:20:30
1:20:30
2025-10-04 18:00

 1:25:17
1:25:17
2025-09-08 18:00

 1:26:28
1:26:28
2025-09-06 18:00

 1:13:52
1:13:52
2025-09-17 18:00

 1:20:52
1:20:52
2025-10-02 18:00

 1:13:30
1:13:30
2025-09-20 18:00

 1:33:38
1:33:38
2025-10-09 18:00

 1:10:48
1:10:48
2025-09-15 18:00

 1:14:10
1:14:10
2025-09-24 18:00

 22:03
22:03
2025-09-21 18:00

 43:30
43:30
2025-10-14 18:00

 1:12:19
1:12:19
2025-09-05 18:00

 44:08
44:08
Девочки из Эквестрии. Пропуск за кулисы для Сансет (2018) / Equestria Girls. Sunset's Backstage Pass
2025-10-03 18:00

 22:30
22:30
2025-09-19 18:00

 1:37:06
1:37:06
2025-10-05 18:00

 1:15:49
1:15:49
2025-09-26 18:00

 22:22
22:22
2025-09-11 18:00
0/0

