
 27:57
27:57
2022-10-24 20:13

 5:30
5:30

 5:30
5:30
2024-07-26 13:50

 39:10
39:10

 39:10
39:10
2024-11-11 09:49

 7:00
7:00

 7:00
7:00
2025-01-19 09:15

 37:50
37:50

 37:50
37:50
2025-09-07 16:00

 5:02
5:02

 5:02
5:02
2025-05-11 10:58

 1:00:44
1:00:44

 1:00:44
1:00:44
2025-09-07 13:08

 26:53
26:53

 26:53
26:53
2023-11-27 22:49
 5:19
5:19

 5:19
5:19
2024-05-04 06:27

 11:15
11:15

 11:15
11:15
2025-09-06 16:00

 10:44
10:44

 10:44
10:44
2023-11-15 09:23

 22:39
22:39

 22:39
22:39
2022-10-24 19:50

 11:19
11:19

 11:19
11:19
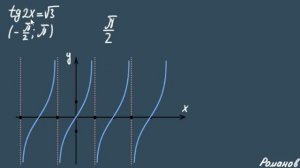
Сдвиг графика тригонометрических функций вдоль осей координат. Преобразование графиков триг. функций
2022-10-24 19:54
 12:25
12:25

 12:25
12:25
2023-09-10 13:47
 6:00
6:00

 6:00
6:00
2023-09-21 11:03

 3:44
3:44

 3:44
3:44
2025-04-30 23:27
![В БОЛЬ? Выпуск №141 КАЛЬКУЛЯТОРНЫЙ ВОИН Объект 140 в Минске [World of Tanks]](https://pic.rutubelist.ru/video/1b/4c/1b4c3ba06434819c9a526fb9f4cb36a8.jpg?width=300)
 15:09
15:09
![В БОЛЬ? Выпуск №141 КАЛЬКУЛЯТОРНЫЙ ВОИН Объект 140 в Минске [World of Tanks]](https://pic.rutubelist.ru/video/1b/4c/1b4c3ba06434819c9a526fb9f4cb36a8.jpg?width=300)
 15:09
15:09
2021-05-31 13:00
 16:10
16:10
![Anette - Erjanik em (Official Video 2025)]() 3:36
3:36
![Игорь Крутой - Зонтик (Премьера клипа 2025)]() 4:00
4:00
![Жалолиддин Ахмадалиев - Тонг отгунча (Премьера клипа 2025)]() 4:44
4:44
![Динара Швец - Новая история (Премьера клипа 2025)]() 3:45
3:45
![Азиз Абдуллох - Аллохнинг айтгани булади (Премьера клипа 2025)]() 3:40
3:40
![Фаррух Хамраев - Отажоним булсайди (Премьера клипа 2025)]() 3:08
3:08
![Magas - Без тебя (Премьера клипа 2025)]() 2:28
2:28
![Lx24 - Сберегу (Премьера клипа 2025)]() 2:57
2:57
![Премьера клипа! Ваня Дмитриенко - Настоящая]() 3:33
3:33
![MILEN - Украду тебя (Премьера 2025)]() 3:40
3:40
![Зафар Эргашов - Мусофирда каридим (Премьера клипа 2025)]() 4:58
4:58
![TASSO - Таю (Премьера клипа 2025)]() 3:23
3:23
![Рустам Батербиев - Пора расстаться (Премьера клипа 2025)]() 2:38
2:38
![Ольга Стельмах – Кафе-Шантан (Премьера клипа 2025)]() 3:02
3:02
![ARTEE - Лети (Премьера клипа 2025)]() 3:13
3:13
![Зара - Я несла свою беду (Премьера клипа 2025)]() 3:36
3:36
![Enrasta, Мурат Тхагалегов - Калым (Премьера клипа 2025)]() 3:07
3:07
![Ганишер Раззоков - Дилижон (Премьера клипа 2025)]() 3:46
3:46
![Ислам Итляшев - Скандал (Премьера клипа 2025)]() 2:08
2:08
![ИЮЛА - Ты был прав (Премьера клипа 2025)]() 2:21
2:21
![Комната (2003)]() 1:39:52
1:39:52
![Большое смелое красивое путешествие (2025)]() 1:49:16
1:49:16
![Терминатор 2: Судный день | Terminator 2: Judgment Day (1991) (Гоблин)]() 2:36:13
2:36:13
![Миссия невыполнима: Финальная расплата (2025)]() 2:52:55
2:52:55
![Неудержимые 3 (2014) 1080]() 2:06:27
2:06:27
![Финикийская схема (2025)]() 1:41:00
1:41:00
![Сирены (2025) Netflix]() 4:26:06
4:26:06
![Посредники]() 2:04:01
2:04:01
![Порочный круг (2025)]() 1:43:41
1:43:41
![Первый день моей жизни]() 1:56:45
1:56:45
![Монстры: История Эда Гейна (2025) (мини-сериал)]() 7:26:60
7:26:60
![Doom (2005) (Расширенная версия)]() 1:52:44
1:52:44
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Плохой Cанта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:28:32
1:28:32
![Тот самый | Him (2025)]() 1:36:20
1:36:20
![Некая справедливость (2014)]() 1:32:52
1:32:52
![Рыжая Соня (2025)]() 1:50:40
1:50:40
![Добыча (2022)]() 1:45:08
1:45:08
![Макс Пэйн (2008) (Расширенная версия)]() 1:42:59
1:42:59
![Девушка из каюты №10 (2025)]() 1:35:13
1:35:13
![Науэль и волшебная книга (2020) / Nauel and the Magic Book]()
 1:37:06
1:37:06
![Дорога домой (2021) / Back to the Outback]()
 1:31:40
1:31:40
![Странные чары (2015) / Strange Magic]()
 1:39:20
1:39:20
![Иллюзионист (2010) / L'illusionniste]()
 1:19:53
1:19:53
![Приключения Десперо (2008) / The Tale of Despereaux]()
 1:33:38
1:33:38
![Альфа и Омега 2: Приключения праздничного воя (2013) / Alpha and Omega 2: A Howl-iday Adventure]()
 45:08
45:08
![Альфа и Омега: Клыкастая братва (2010) / Alpha and Omega]()
 1:27:56
1:27:56
![Альфа и Омега 3: Большие Волчьи Игры (2013) / Alpha and Omega 3: The Great Wolf Games]()
 45:01
45:01
![Шевели ластами 2 (2012) / A Turtle's Tale 2: Sammy's Escape from Paradise]()
 1:32:45
1:32:45
![Земля до начала времён 3: В поисках воды (1995) / The Land Before Time III]()
 1:10:48
1:10:48
![Гномео и Джульетта (2011) / Gnomeo & Juliet]()
 1:23:51
1:23:51
![Земля до начала времён 11: Вторжение Мышезавров (2005) / The Land Before Time XI]()
 1:20:52
1:20:52
![Плохие парни: Жутковатое ограбление (2024) / The Bad Guys: Haunted Heist]()
 22:03
22:03
![Союз зверей (2010) / Animals United]()
 1:33:07
1:33:07
![Шерлок Гномс (2018) / Sherlock Gnomes]()
 1:26:19
1:26:19
![Земля до начала времён 7: Камень Холодного Огня (2000) / The Land Before Time VII]()
 1:14:10
1:14:10
![Альфа и Омега 7: Большое обледенение (2016) / Alpha and Omega 7: The Big Fureeze]()
 45:06
45:06
![Эти прекрасные мультяшки: Рождественский выпуск (1992) / It's a Wonderful Christmas Special]()
 22:22
22:22
![Девочки из Эквестрии. Пропуск за кулисы для Сансет (2018) / Equestria Girls. Sunset's Backstage Pass]()
 44:08
44:08
![Плохие парни: Очень плохой праздник (2023) / The Bad Guys: A Very Bad Holiday]()
 22:30
22:30

 16:10
16:10Скачать видео
| 432x232 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:36
3:36
2025-10-18 10:11
 4:00
4:00
2025-10-18 10:19
 4:44
4:44
2025-10-19 10:46
 3:45
3:45
2025-10-15 10:45
 3:40
3:40
2025-10-18 10:34
 3:08
3:08
2025-10-18 10:28
 2:28
2:28
2025-10-17 12:00
 2:57
2:57
2025-10-11 12:26
 3:33
3:33
2025-10-18 17:45
 3:40
3:40
2025-10-15 11:15
 4:58
4:58
2025-10-18 10:31
 3:23
3:23
2025-10-16 10:00
 2:38
2:38
2025-10-16 11:06
 3:02
3:02
2025-10-11 11:50
 3:13
3:13
2025-10-18 09:47
 3:36
3:36
2025-10-18 10:07
 3:07
3:07
2025-10-11 12:03
 3:46
3:46
2025-10-14 11:30
 2:08
2:08
2025-10-14 10:40
 2:21
2:21
2025-10-18 10:16
0/0
 1:39:52
1:39:52
2025-10-08 18:11
 1:49:16
1:49:16
2025-10-17 13:42
 2:36:13
2:36:13
2025-10-07 09:27
 2:52:55
2:52:55
2025-10-05 20:57
2025-10-15 06:51
 1:41:00
1:41:00
2025-10-05 21:22
 4:26:06
4:26:06
2025-10-12 20:27
 2:04:01
2:04:01
2025-10-13 11:37
 1:43:41
1:43:41
2025-10-13 12:39
 1:56:45
1:56:45
2025-10-13 11:38
 7:26:60
7:26:60
2025-10-05 20:29
 1:52:44
1:52:44
2025-10-09 20:16
 1:35:11
1:35:11
2025-10-13 12:06
 1:28:32
1:28:32
2025-10-07 09:27
 1:36:20
1:36:20
2025-10-09 20:02
2025-10-13 04:45
 1:50:40
1:50:40
2025-10-15 14:11
 1:45:08
1:45:08
2025-10-06 12:51
 1:42:59
1:42:59
2025-10-15 16:40
 1:35:13
1:35:13
2025-10-12 11:54
0/0

 1:37:06
1:37:06
2025-10-05 18:00

 1:31:40
1:31:40
2025-09-12 18:00

 1:39:20
1:39:20
2025-10-13 18:00

 1:19:53
1:19:53
2025-10-11 18:00

 1:33:38
1:33:38
2025-10-09 18:00

 45:08
45:08
2025-10-08 18:00

 1:27:56
1:27:56
2025-09-16 18:00

 45:01
45:01
2025-10-10 18:00

 1:32:45
1:32:45
2025-10-17 18:02

 1:10:48
1:10:48
2025-09-15 18:00

 1:23:51
1:23:51
2025-09-10 18:00

 1:20:52
1:20:52
2025-10-02 18:00

 22:03
22:03
2025-09-21 18:00

 1:33:07
1:33:07
2025-10-15 18:01

 1:26:19
1:26:19
2025-09-25 18:00

 1:14:10
1:14:10
2025-09-24 18:00

 45:06
45:06
2025-10-18 18:00

 22:22
22:22
2025-09-11 18:00

 44:08
44:08
Девочки из Эквестрии. Пропуск за кулисы для Сансет (2018) / Equestria Girls. Sunset's Backstage Pass
2025-10-03 18:00

 22:30
22:30
2025-09-19 18:00
0/0

