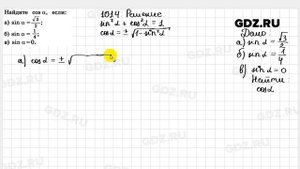
 2:55
2:55
2023-12-28 17:57

 40:31
40:31

 40:31
40:31
2024-08-22 15:11

 3:50
3:50

 3:50
3:50
2023-12-28 15:12
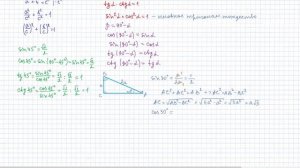
 33:57
33:57

 33:57
33:57
2023-12-22 08:33

 5:16
5:16

 5:16
5:16
2023-12-28 15:13

 33:21
33:21

 33:21
33:21
2025-08-22 20:12

 3:44
3:44

 3:44
3:44
2023-12-28 13:37
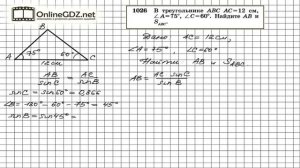
 5:26
5:26

 5:26
5:26
2023-12-28 13:21
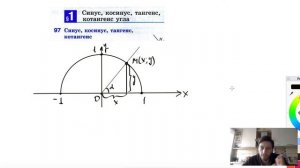
 3:28
3:28

 3:28
3:28
2024-06-07 13:26

 3:30
3:30

 3:30
3:30
2024-11-07 11:30

 4:20
4:20

 4:20
4:20
2025-03-10 03:53

 28:57
28:57

 28:57
28:57
2023-09-10 13:17

 7:03
7:03

 7:03
7:03
2023-09-11 21:40

 4:46
4:46

 4:46
4:46
2023-09-11 15:37
 38:56
38:56

 38:56
38:56
2023-09-27 02:10

 14:59
14:59

 14:59
14:59
2023-09-25 02:23

 7:15
7:15

 7:15
7:15
2023-09-25 22:22

 8:42
8:42
![Taylor Swift - The Fate of Ophelia (Official Video 2025)]() 3:58
3:58
![Ольга Бузова - Не надо (Премьера клипа 2025)]() 3:15
3:15
![МАРАТ & АРНИ - Стала женой (Премьера клипа 2025)]() 3:51
3:51
![Премьера клипа! Ваня Дмитриенко - Настоящая]() 3:33
3:33
![MEDNA - Алё (Премьера клипа 2025)]() 2:28
2:28
![Наталья Влади - А я такая (Премьера клипа 2025)]() 2:21
2:21
![Любовь Попова - Прощай (Премьера клипа 2025)]() 3:44
3:44
![Мария Зайцева - Жаль моя (Премьера клипа 2025)]() 4:25
4:25
![Ислам Итляшев - Скандал (Премьера клипа 2025)]() 2:08
2:08
![Анна Бершадская - Новая я (Премьера клипа 2025)]() 2:41
2:41
![Zhamil Turan - Капали (Премьера клипа 2025)]() 3:08
3:08
![KINO - DIRTY BOY (Feat. JAMIE, UWA)]() 3:22
3:22
![Игорь Кибирев - Пьяная ночь (Премьера клипа 2025)]() 3:08
3:08
![Рейсан Магомедкеримов - Забываю (Премьера клипа 2025)]() 3:20
3:20
![ARTIX, SHAXO - Дождь (Премьера клипа 2025)]() 5:23
5:23
![Дана Лахова - Одинокая луна (Премьера клипа 2025)]() 2:15
2:15
![Артур Пирожков - ALARM (Премьера клипа 2025)]() 3:22
3:22
![Anette - Erjanik em (Official Video 2025)]() 3:36
3:36
![MARSO - Дура (Премьера клипа 2025)]() 3:05
3:05
![Жалолиддин Ахмадалиев - Тонг отгунча (Премьера клипа 2025)]() 4:44
4:44
![Актер | The Actor (2025)]() 1:38:13
1:38:13
![Моя мертвая подруга Зои | My Dead Friend Zoe (2024)]() 1:42:40
1:42:40
![Опустошение | Havoc (2025)]() 1:47:26
1:47:26
![Долина эха | Echo Valley (2025)]() 1:44:37
1:44:37
![Мир юрского периода Возрождение | Jurassic World: Rebirth (2025)]() 2:13:53
2:13:53
![Электрический штат | The Electric State (2025)]() 2:08:34
2:08:34
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Как приручить дракона | How to Train Your Dragon (2025)]() 2:05:23
2:05:23
![Углубление (2025)]() 2:07:52
2:07:52
![Хани, не надо! | Honey Don't! (2025)]() 1:29:32
1:29:32
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Сверху вниз | Highest 2 Lowest (2025)]() 2:13:21
2:13:21
![Вульфмен | Wolf Man (2025)]() 1:42:55
1:42:55
![Кирпич | Brick]() 1:40:58
1:40:58
![Соник 3 в кино | Sonic the Hedgehog 3 (2024)]() 1:50:21
1:50:21
![Бастион 36 | Bastion 36 (2025)]() 2:04:58
2:04:58
![Город демонов | Oni Goroshi (2025)]() 1:48:12
1:48:12
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Раст | Rust (2024)]() 2:19:54
2:19:54
![Тодли Великолепный!]() 3:15
3:15
![Простоквашино]() 6:48
6:48
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Супер Зак]() 11:38
11:38
![Мартышкины]() 7:09
7:09
![Таинственные золотые города]() 23:04
23:04
![Агент 203]() 21:08
21:08
![МиниФорс]() 0:00
0:00
![Чемпионы]() 7:21
7:21
![Умка]() 7:11
7:11
![Корги по имени Моко. Домашние животные]() 1:13
1:13
![Пиратская школа]() 11:06
11:06
![Забавные медвежата]() 13:00
13:00
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:21
10:21
![Мультфильмы военных лет | Специальный проект к 80-летию Победы]() 7:20
7:20
![Приключения Пети и Волка]() 11:00
11:00
![Пластилинки]() 25:31
25:31
![Зебра в клеточку]() 6:30
6:30
![Новогодние мультики – Союзмультфильм]() 7:04
7:04

 8:42
8:42Скачать видео
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:58
3:58
2025-10-17 11:48
 3:15
3:15
2025-10-18 10:02
 3:51
3:51
2025-10-16 11:41
 3:33
3:33
2025-10-18 17:45
 2:28
2:28
2025-10-21 09:22
 2:21
2:21
2025-10-14 11:07
 3:44
3:44
2025-10-21 09:25
 4:25
4:25
2025-10-17 11:28
 2:08
2:08
2025-10-14 10:40
 2:41
2:41
2025-10-22 14:02
 3:08
3:08
2025-10-22 14:26
2025-10-13 16:08
 3:08
3:08
2025-10-16 11:32
 3:20
3:20
2025-10-16 11:19
 5:23
5:23
2025-10-14 11:01
 2:15
2:15
2025-10-22 14:16
 3:22
3:22
2025-10-20 14:44
 3:36
3:36
2025-10-18 10:11
 3:05
3:05
2025-10-17 11:37
 4:44
4:44
2025-10-19 10:46
0/0
 1:38:13
1:38:13
2025-04-09 20:04
 1:42:40
1:42:40
2025-05-16 16:49
 1:47:26
1:47:26
2025-08-02 13:33
 1:44:37
1:44:37
2025-08-03 10:47
 2:13:53
2:13:53
2025-08-09 11:00
 2:08:34
2:08:34
2025-03-21 19:58
 1:29:27
1:29:27
2025-09-07 22:44
 1:54:40
1:54:40
2025-09-24 11:35
 2:05:23
2:05:23
2025-07-18 18:28
 2:07:52
2:07:52
2025-02-18 18:05
 1:29:32
1:29:32
2025-09-15 11:39
 2:15:54
2:15:54
2025-10-13 19:02
 2:13:21
2:13:21
2025-09-09 12:49
 1:42:55
1:42:55
2025-02-06 16:11
 1:40:58
1:40:58
2025-08-03 10:48
 1:50:21
1:50:21
2025-01-23 19:58
 2:04:58
2:04:58
2025-04-26 17:36
 1:48:12
1:48:12
2025-08-12 17:48
 1:35:11
1:35:11
2025-10-13 12:06
 2:19:54
2:19:54
2025-05-12 21:51
0/0
 3:15
3:15
2025-06-10 13:56
 6:48
6:48
2025-10-17 10:00
2021-09-22 23:36
2021-09-22 22:07
 7:09
7:09
2025-04-01 16:06
 23:04
23:04
2025-01-09 17:26
 21:08
21:08
2025-01-09 16:39
 0:00
0:00
2025-10-22 22:36
 7:21
7:21
2025-10-07 09:00
 7:11
7:11
2025-01-13 11:05
 1:13
1:13
2024-11-29 14:40
 11:06
11:06
2022-04-01 15:56
 13:00
13:00
2024-12-02 13:15
 13:00
13:00
2024-11-28 16:19
 10:21
10:21
2025-09-11 10:05
 7:20
7:20
2025-05-03 12:34
 11:00
11:00
2022-04-01 17:59
 25:31
25:31
2022-04-01 14:30
 6:30
6:30
2022-03-31 13:09
 7:04
7:04
2023-07-25 00:09
0/0

