
 4:11
4:11
2025-02-03 16:30

 5:21
5:21

 5:21
5:21
2025-02-03 16:00

 15:32
15:32

 15:32
15:32
2024-05-17 13:38

 3:49
3:49

 3:49
3:49
2024-01-14 20:41

 7:47
7:47

 7:47
7:47
2024-10-10 15:17
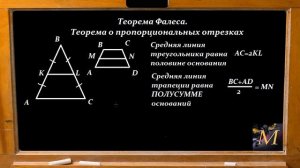
 13:26
13:26

 13:26
13:26
2023-12-28 12:50

 24:13
24:13

 24:13
24:13
2024-11-02 08:58

 8:08
8:08

 8:08
8:08
2023-12-28 13:01

 7:19
7:19

 7:19
7:19
2023-12-22 19:18
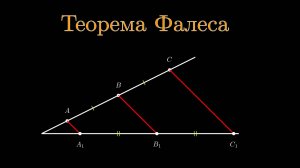
 4:40
4:40

 4:40
4:40
2025-09-07 11:52

 10:27
10:27

 10:27
10:27
2025-05-13 09:08

 11:34
11:34

 11:34
11:34
2020-09-25 17:43

 5:38
5:38

 5:38
5:38
2023-09-01 14:36
 2:06
2:06

 2:06
2:06
2023-09-22 21:48
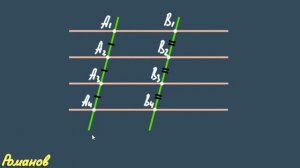
 3:12
3:12

 3:12
3:12
2023-09-11 13:28

 6:00
6:00

 6:00
6:00
2018-05-31 11:47

 7:27
7:27

 7:27
7:27
2022-03-15 10:53
 13:10
13:10
![Ольга Бузова - Не надо (Премьера клипа 2025)]() 3:15
3:15
![KhaliF - Где бы не был я (Премьера клипа 2025)]() 2:53
2:53
![Азиз Абдуллох - Аллохнинг айтгани булади (Премьера клипа 2025)]() 3:40
3:40
![MEDNA - Алё (Премьера клипа 2025)]() 2:28
2:28
![Рустам Нахушев, Зульфия Чотчаева - Каюсь (Премьера клипа 2025)]() 3:20
3:20
![Зара - Я несла свою беду (Премьера клипа 2025)]() 3:36
3:36
![Шерзодбек Жонибеков - Дадажон (Премьера клипа 2025)]() 3:02
3:02
![Сергей Завьялов - В дороге (Премьера клипа 2025)]() 3:14
3:14
![Ислам Итляшев - Не вспоминай (Премьера клипа 2025)]() 2:52
2:52
![SHAXO - Негодяйка (Премьера клипа 2025)]() 3:27
3:27
![INSTASAMKA - BOSS (Премьера клипа 2025)]() 3:41
3:41
![Рейсан Магомедкеримов, Ренат Омаров - Бла-та-та (Премьера клипа 2025)]() 2:26
2:26
![ИЮЛА - Ты был прав (Премьера клипа 2025)]() 2:21
2:21
![Артур Халатов - Девочка моя (Премьера клипа 2025)]() 2:37
2:37
![Anette - Erjanik em (Official Video 2025)]() 3:36
3:36
![Инна Вальтер - Роза (Премьера клипа 2025)]() 3:18
3:18
![Дана Лахова - Одинокая луна (Премьера клипа 2025)]() 2:15
2:15
![Бьянка - Бренд (Премьера клипа 2025)]() 2:29
2:29
![Сардор Расулов - Етолмадим (Премьера клипа 2025)]() 4:15
4:15
![SERYABKINA, Брутто - Светофоры (Премьера клипа 2025)]() 3:49
3:49
![Сумерки | Twilight (2008)]() 2:01:55
2:01:55
![Свинтусы | The Twits (2025)]() 1:42:50
1:42:50
![Положитесь на Пита | Lean on Pete (2017)]() 2:02:04
2:02:04
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![F1 (2025)]() 2:35:53
2:35:53
![Голый пистолет | The Naked Gun (2025)]() 1:26:24
1:26:24
![Диспетчер | Relay (2025)]() 1:51:56
1:51:56
![Мужчина у меня в подвале | The Man in My Basement (2025)]() 1:54:48
1:54:48
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Счастливчик Гилмор 2 | Happy Gilmore (2025)]() 1:57:36
1:57:36
![Элис, дорогая | Alice, Darling (2022)]() 1:29:30
1:29:30
![Порочный круг | Vicious (2025)]() 1:42:30
1:42:30
![Плохие парни 2 | The Bad Guys 2 (2025)]() 1:43:51
1:43:51
![Плюшевый пузырь | The Beanie Bubble (2023)]() 1:50:15
1:50:15
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Непрощённая | The Unforgivable (2021)]() 1:54:10
1:54:10
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![Когда ты закончишь спасать мир | When You Finish Saving the World (2022)]() 1:27:40
1:27:40
![Вечеринка только начинается | The Party's Just Beginning (2018)]() 1:31:20
1:31:20
![Хани, не надо! | Honey Don't! (2025)]() 1:29:32
1:29:32
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Пиратская школа]() 11:06
11:06
![Забавные медвежата]() 13:00
13:00
![Пип и Альба Сезон 1]() 11:02
11:02
![Папа Супергерой Сезон 1]() 4:28
4:28
![Тайны Медовой долины]() 7:01
7:01
![Чемпионы]() 7:21
7:21
![Роботы-пожарные]() 12:31
12:31
![Хвостатые песенки]() 7:00
7:00
![Простоквашино. Финансовая грамотность]() 3:27
3:27
![Сборники «Зебра в клеточку»]() 45:30
45:30
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Паровозик Титипо]() 13:42
13:42
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Последний книжный магазин]() 11:20
11:20
![МиниФорс]() 0:00
0:00
![Монсики]() 6:30
6:30
![Таинственные золотые города]() 23:04
23:04

 13:10
13:10Скачать видео
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:15
3:15
2025-10-18 10:02
 2:53
2:53
2025-10-28 12:16
 3:40
3:40
2025-10-18 10:34
 2:28
2:28
2025-10-21 09:22
 3:20
3:20
2025-10-30 10:39
 3:36
3:36
2025-10-18 10:07
 3:02
3:02
2025-10-25 13:03
 3:14
3:14
2025-10-29 10:28
 2:52
2:52
2025-10-28 10:47
 3:27
3:27
2025-10-28 11:18
 3:41
3:41
2025-10-23 13:04
 2:26
2:26
2025-10-22 14:10
 2:21
2:21
2025-10-18 10:16
 2:37
2:37
2025-10-28 10:22
 3:36
3:36
2025-10-18 10:11
 3:18
3:18
2025-10-28 10:36
 2:15
2:15
2025-10-22 14:16
 2:29
2:29
2025-10-25 12:48
 4:15
4:15
2025-10-26 12:52
 3:49
3:49
2025-10-25 12:52
0/0
 2:01:55
2:01:55
2025-08-28 15:32
 1:42:50
1:42:50
2025-10-21 16:19
 2:02:04
2:02:04
2025-08-27 17:17
 1:35:11
1:35:11
2025-10-13 12:06
 2:35:53
2:35:53
2025-08-26 11:45
 1:26:24
1:26:24
2025-09-03 13:20
 1:51:56
1:51:56
2025-09-24 11:35
 1:54:48
1:54:48
2025-10-01 15:17
 2:09:55
2:09:55
2025-10-05 00:32
 1:57:36
1:57:36
2025-08-21 17:43
 1:29:30
1:29:30
2025-09-11 08:20
 1:42:30
1:42:30
2025-10-14 20:27
 1:43:51
1:43:51
2025-08-26 16:18
 1:50:15
1:50:15
2025-08-27 18:32
 2:02:20
2:02:20
2025-10-01 12:06
 1:54:10
1:54:10
2025-08-27 17:17
 1:29:27
1:29:27
2025-09-07 22:44
 1:27:40
1:27:40
2025-08-27 17:17
 1:31:20
1:31:20
2025-08-27 17:17
 1:29:32
1:29:32
2025-09-15 11:39
0/0
2021-09-22 22:45
 11:06
11:06
2022-04-01 15:56
 13:00
13:00
2024-12-02 13:15
2021-09-22 23:37
2021-09-22 21:52
 7:01
7:01
2022-03-30 17:25
 7:21
7:21
2025-10-07 09:00
2021-09-23 00:12
 7:00
7:00
2025-06-01 11:15
 3:27
3:27
2024-12-07 11:00
 45:30
45:30
2025-09-17 18:49
 4:33
4:33
2024-12-17 16:56
2021-09-22 23:36
2021-09-22 20:39
 13:42
13:42
2024-11-28 14:12
2021-09-22 21:49
 11:20
11:20
2025-09-12 10:05
 0:00
0:00
2025-10-31 22:12
 6:30
6:30
2022-03-29 19:16
 23:04
23:04
2025-01-09 17:26
0/0

