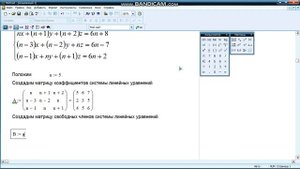
 8:27
8:27
2023-08-26 15:50
![Прямой эфир ТНТ]() 0:00
0:00
 0:00
0:00
2019-06-06 10:44
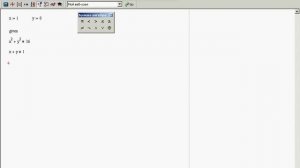
 2:45
2:45

 2:45
2:45
2023-09-26 08:41
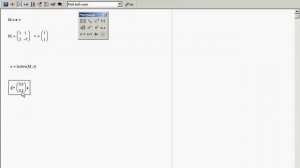
 2:23
2:23

 2:23
2:23
2023-09-20 05:35
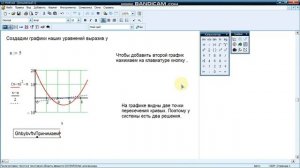
 8:25
8:25

 8:25
8:25
2023-09-09 15:46

 1:57:01
1:57:01

 1:57:01
1:57:01
2025-12-06 21:00

 2:26:17
2:26:17

 2:26:17
2:26:17
2025-12-12 14:18

 1:38:14
1:38:14

 1:38:14
1:38:14
2025-12-11 16:08

 2:13:55
2:13:55

 2:13:55
2:13:55
2025-11-30 20:55

 2:34:37
2:34:37

 2:34:37
2:34:37
2025-12-11 18:59

 2:32:19
2:32:19

 2:32:19
2:32:19
2023-09-10 18:25

 2:16:26
2:16:26

 2:16:26
2:16:26
2025-12-12 12:26

 2:41:27
2:41:27

 2:41:27
2:41:27
2025-12-05 19:24

 1:48:45
1:48:45

 1:48:45
1:48:45
2023-09-26 22:34

 1:03:11
1:03:11

 1:03:11
1:03:11
2025-12-10 19:01

 11:59:14
11:59:14

 11:59:14
11:59:14
2025-12-11 08:06

 1:37:23
1:37:23

 1:37:23
1:37:23
2025-12-06 19:14

 1:42:55
1:42:55
![NLO, Leonid Rudenko - Зеленоглазое такси (Премьера клипа 2025)]() 2:22
2:22
![Женя Белоусова - Мы больше не рядом (Премьера клипа 2025)]() 2:50
2:50
![SHAXO - Рандеву (Премьера клипа 2025)]() 3:37
3:37
![NAIMAN - Хулиганка (Премьера клипа 2025)]() 2:26
2:26
![Зардияна - Севган бахтли буларму (Премьера клипа 2025)]() 3:28
3:28
![Антон и Альфия - Ойся, ты ойся (Премьера клипа 2025)]() 3:04
3:04
![Макс Вертиго, PAKALENA - Разбиться о скалы (Премьера клипа 2025)]() 3:18
3:18
![Ruslan Bakinskiy & Vuqar Islam - Я Забыл (Премьера клипа 2025)]() 4:01
4:01
![Adil - Любит она (Премьера клипа 2025)]() 2:49
2:49
![Ахрорбек Хурсаналиев - Йигитнинг гами (Премьера клипа 2025)]() 6:09
6:09
![140 ударов в минуту – Мне тебя так мало (Премьера клипа 2025)]() 3:44
3:44
![Aymar Zairov - И только дым от сигарет (Премьера клипа 2025)]() 3:41
3:41
![Зареена Заирова - Ман кетаман (Премьера клипа 2025)]() 5:08
5:08
![Zhamil Turan - Ты не моя (Премьера клипа 2025)]() 2:37
2:37
![Альберт Эркенов - Мои шрамы (Премьера клипа 2025)]() 3:15
3:15
![Артур Бесаев - Все пройдет (Премьера клипа 2025)]() 3:44
3:44
![Евгений Путилов - Веришь - не веришь (Премьера клипа 2025)]() 3:43
3:43
![Руслан Добрый - Всё прошло (Премьера клипа 2025)]() 2:24
2:24
![Жанна Аркадьевна - Мой тренер (Премьера клипа 2025)]() 2:14
2:14
![Асия - Дом (Премьера клипа 2025)]() 6:45
6:45
![После охоты | After the Hunt (2025)]() 2:20:25
2:20:25
![Paзpушитeль миpoв | Worldbreaker (2025)]() 1:34:45
1:34:45
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Все дьяволы здесь | All the Devils are Here (2025)]() 1:31:39
1:31:39
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Супергеройское кино | Superhero Movie (2008)]() 1:22:33
1:22:33
![Семейный план 2 | The Family Plan 2 (2025)]() 1:46:14
1:46:14
![Чёрный телефон 2 | Black Phone 2 (2025)]() 1:53:55
1:53:55
![Стив | Steve (2025)]() 1:33:34
1:33:34
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Богомол | Samagwi (2025)]() 1:53:29
1:53:29
![Хищник | Predator (1987) (Гоблин)]() 1:46:40
1:46:40
![Только ты | All of You (2025)]() 1:38:22
1:38:22
![Бугония | Bugonia (2025)]() 1:59:12
1:59:12
![Баллада о маленьком игроке | Ballad of a Small Player (2025)]() 1:42:60
1:42:60
![Рука, качающая колыбель | The Hand That Rocks the Cradle (2025)]() 1:44:57
1:44:57
![Гедда | Hedda (2025)]() 1:48:23
1:48:23
![Боже. Как. Смешно. | Oh. What. Fun. (2025)]() 1:47:58
1:47:58
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Сборники «Зебра в клеточку»]() 45:30
45:30
![Сборники «Ну, погоди!»]() 1:10:01
1:10:01
![Чемпионы]() 7:15
7:15
![Котёнок Шмяк]() 11:04
11:04
![Простоквашино. Финансовая грамотность]() 3:27
3:27
![Оранжевая корова]() 6:30
6:30
![Команда Дино Сезон 1]() 12:08
12:08
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Полли Покет Сезон 1]() 21:30
21:30
![Агент 203]() 21:08
21:08
![Команда Дино Сезон 2]() 12:31
12:31
![Сборники «Умка»]() 3:09:60
3:09:60
![Корги по имени Моко. Домашние животные]() 1:13
1:13
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Панда и петушок Лука]() 12:12
12:12
![Минифорс. Сила динозавров]() 12:51
12:51
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Монсики]() 6:30
6:30
![Новогодние мультики – Союзмультфильм]() 7:04
7:04

 1:42:55
1:42:55Скачать Видео с Рутуба / RuTube
| 320x240 | ||
| 480x360 | ||
| 640x480 | ||
| 960x720 |
 2:22
2:22
2025-12-08 15:50
 2:50
2:50
2025-12-04 11:41
 3:37
3:37
2025-12-09 13:50
 2:26
2:26
2025-12-09 13:27
 3:28
3:28
2025-12-04 12:09
 3:04
3:04
2025-12-08 19:50
 3:18
3:18
2025-12-04 11:49
 4:01
4:01
2025-12-10 10:13
 2:49
2:49
2025-12-04 11:33
 6:09
6:09
2025-12-11 10:43
 3:44
3:44
2025-12-10 12:30
 3:41
3:41
2025-12-02 10:34
 5:08
5:08
2025-12-11 10:33
 2:37
2:37
2025-12-04 11:11
 3:15
3:15
2025-12-08 19:45
 3:44
3:44
2025-12-10 00:19
 3:43
3:43
2025-12-06 15:51
 2:24
2:24
2025-12-11 01:31
 2:14
2:14
2025-12-08 15:58
 6:45
6:45
2025-11-29 13:44
0/0
 2:20:25
2:20:25
2025-11-27 19:24
 1:34:45
1:34:45
2025-11-27 19:40
 2:15:54
2:15:54
2025-10-13 19:02
 1:31:39
1:31:39
2025-10-02 20:46
 1:47:25
1:47:25
2025-11-27 03:58
 1:18:55
1:18:55
2025-11-21 14:16
 1:22:33
1:22:33
2025-11-21 14:16
 1:46:14
1:46:14
2025-11-26 06:44
 1:53:55
1:53:55
2025-11-05 19:47
 1:33:34
1:33:34
2025-10-08 12:27
 2:09:55
2:09:55
2025-10-05 00:32
 1:53:29
1:53:29
2025-10-01 12:06
 1:46:40
1:46:40
2025-10-07 09:27
 1:38:22
1:38:22
2025-10-01 12:16
 1:59:12
1:59:12
2025-11-29 02:45
 1:42:60
1:42:60
2025-10-31 10:53
 1:44:57
1:44:57
2025-10-29 16:30
 1:48:23
1:48:23
2025-11-05 19:47
 1:47:58
1:47:58
2025-12-09 13:32
 2:32:29
2:32:29
2025-11-17 11:22
0/0
 45:30
45:30
2025-12-11 18:53
 1:10:01
1:10:01
2025-07-25 20:16
 7:15
7:15
2025-12-10 10:00
 11:04
11:04
2023-05-18 16:41
 3:27
3:27
2024-12-07 11:00
 6:30
6:30
2022-03-31 18:49
2021-09-22 22:29
 13:00
13:00
2024-11-28 16:19
2021-09-22 23:09
 21:08
21:08
2025-01-09 16:39
2021-09-22 22:40
 3:09:60
3:09:60
2025-12-11 18:53
 1:13
1:13
2024-11-29 14:40
2021-09-22 21:03
2021-09-22 21:49
 12:12
12:12
2024-11-29 14:21
 12:51
12:51
2024-11-27 16:39
2021-09-22 20:39
 6:30
6:30
2022-03-29 19:16
 7:04
7:04
2023-07-25 00:09
0/0

