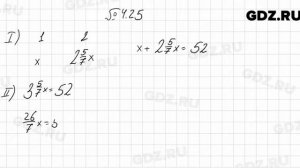
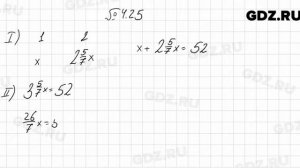 1:50
1:50
2024-09-11 19:52

 10:37
10:37

 10:37
10:37
2024-01-11 16:56

 7:19
7:19

 7:19
7:19
2025-09-24 15:35

 7:40
7:40

 7:40
7:40
2025-09-25 17:00

 3:51
3:51

 3:51
3:51
2025-08-01 13:42

 2:39
2:39

 2:39
2:39
2025-08-01 13:44

 2:15
2:15

 2:15
2:15
2025-09-25 22:19

 23:31
23:31

 23:31
23:31
2025-09-28 11:00

 1:06:32
1:06:32

 1:06:32
1:06:32
2025-09-16 12:56

 1:23:24
1:23:24

 1:23:24
1:23:24
2025-09-18 12:00

 8:30
8:30

 8:30
8:30
2025-09-12 15:00

 3:20
3:20

 3:20
3:20
2025-09-11 10:37

 1:57:38
1:57:38

 1:57:38
1:57:38
2025-09-15 15:22

 5:52
5:52

 5:52
5:52
2025-09-25 23:50

 16:17
16:17

 16:17
16:17
2025-09-17 18:32

 34:56
34:56

 34:56
34:56
2025-09-12 16:44

 4:18
4:18

 4:18
4:18
2025-09-21 11:49

 19:12
19:12
![Эльдар Агачев - Путник (Премьера клипа 2025)]() 3:14
3:14
![Хушнуд - Бевафо ёр (Премьера клипа 2025)]() 5:39
5:39
![Enrasta - Франция (Премьера клипа 2025)]() 2:44
2:44
![Абрикоса, GOSHU - Удали из памяти (Премьера клипа 2025)]() 4:59
4:59
![Мужик из СИБИРИ (Александр Конев) - Поцелуи осени (Премьера клипа 2025)]() 2:59
2:59
![Ислам Итляшев - Не реви (Премьера клипа 2025)]() 2:41
2:41
![UMARO - 1-2-3 (Премьера клипа 2025)]() 2:52
2:52
![Фрося - На столике (Премьера клипа 2025)]() 1:42
1:42
![Аброр Киличов - Тим-Тим (Премьера клипа 2025)]() 4:42
4:42
![Шавкат Зулфикор & Нурзида Исаева - Одамнинг ёмони ёмон буларкан (Премьера клипа 2025)]() 8:21
8:21
![Бекзод Хаккиев - Айтаман (Премьера клипа 2025)]() 2:41
2:41
![Женя Белоусова - Раненая птица (Премьера клипа 2025)]() 2:47
2:47
![АКУЛИЧ - Красные глаза (Премьера клипа 2025)]() 2:13
2:13
![Шамиль Кашешов - Когда мы встретились с тобой (Премьера клипа 2025)]() 3:10
3:10
![ZIMMA - Город Тает (Премьера клипа 2025)]() 2:30
2:30
![Ozoda - Chamadon (Official Video 2025)]() 5:23
5:23
![Жамоладдин Аматов - Окибат (Премьера клипа 2025)]() 4:38
4:38
![ARTEE - Ты моя (Премьера клипа 2025)]() 3:31
3:31
![Владимир Ждамиров, Игорь Кибирев - Тик так (Премьера 2025)]() 3:30
3:30
![ZAMA - Глаза цвета кофе (Премьера клипа 2025)]() 2:57
2:57
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Стив | Steve (2025)]() 1:33:34
1:33:34
![Чумовая пятница 2 | Freakier Friday (2025)]() 1:50:38
1:50:38
![Диспетчер | Relay (2025)]() 1:51:56
1:51:56
![Святые из Бундока | The Boondock Saints (1999) (Гоблин)]() 1:48:30
1:48:30
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Терминатор 2: Судный день | Terminator 2: Judgment Day (1991) (Гоблин)]() 2:36:13
2:36:13
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Супруги Роуз | The Roses (2025)]() 1:45:29
1:45:29
![Свайпнуть | Swiped (2025)]() 1:50:35
1:50:35
![Код 3 | Code 3 (2025)]() 1:39:56
1:39:56
![Плохой Cанта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:28:32
1:28:32
![Мужчина у меня в подвале | The Man in My Basement (2025)]() 1:54:48
1:54:48
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Хищник | Predator (1987) (Гоблин)]() 1:46:40
1:46:40
![Дом из динамита | A House of Dynamite (2025)]() 1:55:08
1:55:08
![Цельнометаллическая оболочка | Full Metal Jacket (1987) (Гоблин)]() 1:56:34
1:56:34
![Тот самый | Him (2025)]() 1:36:20
1:36:20
![Протокол выхода | Exit Protocol (2025)]() 1:24:45
1:24:45
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Забавные медвежата]() 13:00
13:00
![Отряд А. Игрушки-спасатели]() 13:06
13:06
![Неодети]() 11:27
11:27
![Команда Дино. Исследователи Сезон 2]() 13:26
13:26
![Пиратская школа]() 11:06
11:06
![Паровозик Титипо]() 13:42
13:42
![Мотофайтеры]() 13:10
13:10
![Лудлвилль]() 7:09
7:09
![Зебра в клеточку]() 6:30
6:30
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Тайны Медовой долины]() 7:01
7:01
![Пип и Альба Сезон 1]() 11:02
11:02
![Енотки]() 7:04
7:04
![Котёнок Шмяк]() 11:04
11:04
![Таинственные золотые города]() 23:04
23:04
![Умка]() 7:11
7:11
![Школьный автобус Гордон]() 12:34
12:34
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:46
10:46
![Приключения Пети и Волка]() 11:00
11:00
![Сборники «Зебра в клеточку»]() 45:30
45:30

 19:12
19:12Скачать Видео с Рутуба / RuTube
| 256x120 | ||
| 432x208 | ||
| 640x312 | ||
| 856x416 |
 3:14
3:14
2025-11-12 12:52
 5:39
5:39
2025-11-23 13:40
 2:44
2:44
2025-11-20 21:37
 4:59
4:59
2025-11-15 12:21
 2:59
2:59
2025-11-21 13:10
 2:41
2:41
2025-11-18 12:35
 2:52
2:52
2025-11-14 12:21
 1:42
1:42
2025-11-12 12:55
 4:42
4:42
2025-11-17 14:30
 8:21
8:21
2025-11-17 14:27
 2:41
2:41
2025-11-17 14:22
 2:47
2:47
2025-11-11 17:49
 2:13
2:13
2025-11-15 12:35
 3:10
3:10
2025-11-22 12:41
 2:30
2:30
2025-11-21 13:20
 5:23
5:23
2025-11-21 13:15
 4:38
4:38
2025-11-11 17:38
 3:31
3:31
2025-11-14 19:59
 3:30
3:30
2025-11-13 11:12
 2:57
2:57
2025-11-13 11:03
0/0
 1:18:55
1:18:55
2025-11-21 14:16
 1:33:34
1:33:34
2025-10-08 12:27
 1:50:38
1:50:38
2025-10-16 16:08
 1:51:56
1:51:56
2025-09-24 11:35
 1:48:30
1:48:30
2025-09-23 22:53
 2:09:55
2:09:55
2025-10-05 00:32
 2:36:13
2:36:13
2025-10-07 09:27
 2:02:20
2:02:20
2025-10-01 12:06
 1:45:29
1:45:29
2025-10-23 18:26
 1:50:35
1:50:35
2025-09-24 10:48
 1:39:56
1:39:56
2025-10-02 20:46
 1:28:32
1:28:32
2025-10-07 09:27
 1:54:48
1:54:48
2025-10-01 15:17
 1:54:40
1:54:40
2025-09-24 11:35
 1:46:40
1:46:40
2025-10-07 09:27
 1:55:08
1:55:08
2025-10-29 16:30
 1:56:34
1:56:34
2025-09-23 22:53
 1:36:20
1:36:20
2025-10-09 20:02
 1:24:45
1:24:45
2025-11-13 23:26
 2:32:29
2:32:29
2025-11-17 11:22
0/0
 13:00
13:00
2024-12-02 13:15
 13:06
13:06
2024-11-28 16:30
 11:27
11:27
2025-10-10 18:25
2021-09-22 22:54
 11:06
11:06
2022-04-01 15:56
 13:42
13:42
2024-11-28 14:12
 13:10
13:10
2024-11-27 14:57
 7:09
7:09
2023-07-06 19:20
 6:30
6:30
2022-03-31 13:09
 3:28
3:28
2025-01-09 17:01
 7:01
7:01
2022-03-30 17:25
2021-09-22 23:37
 7:04
7:04
2022-03-29 18:22
 11:04
11:04
2023-05-18 16:41
 23:04
23:04
2025-01-09 17:26
 7:11
7:11
2025-01-13 11:05
 12:34
12:34
2024-12-02 14:42
 10:46
10:46
2022-06-07 11:02
 11:00
11:00
2022-04-01 17:59
 45:30
45:30
2025-09-17 18:49
0/0
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
