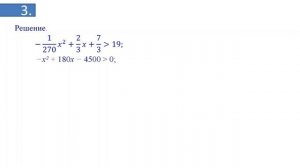
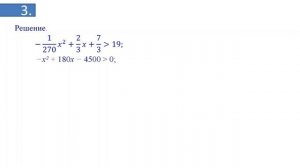 11:06
11:06
2023-12-23 10:53

 49:51
49:51

 49:51
49:51
2024-10-02 15:57

 1:01:35
1:01:35

 1:01:35
1:01:35
2024-09-25 19:21

 1:32:37
1:32:37

 1:32:37
1:32:37
2024-11-28 13:51

 26:01
26:01

 26:01
26:01
2024-09-26 19:17

 2:21:03
2:21:03

 2:21:03
2:21:03
2024-09-29 21:40

 29:05
29:05

 29:05
29:05
2024-09-26 12:57

 1:09:36
1:09:36

 1:09:36
1:09:36
2024-09-25 17:56

 1:00:03
1:00:03

 1:00:03
1:00:03
2024-10-01 16:05

 1:11:49
1:11:49

 1:11:49
1:11:49
2024-10-02 21:00

 30:22
30:22

 30:22
30:22
2024-09-29 12:00

 32:10
32:10

 32:10
32:10
2024-09-30 11:00

 2:02:01
2:02:01

 2:02:01
2:02:01
2024-09-29 23:00

 27:00
27:00

 27:00
27:00
2024-10-01 01:30

 45:46
45:46

 45:46
45:46
2024-09-30 17:31
![ДАР УБЕЖДЕНИЯ | НАДЕЖДА СЫСОЕВА]() 49:20
49:20
 49:20
49:20
2024-10-02 17:03

 39:25
39:25

 39:25
39:25
2024-09-27 15:00

 1:14:48
1:14:48
![Шерзодбек Ишмуратов - Биринчим (Премьера клипа 2025)]() 4:44
4:44
![Bruno Mars ft. Ed Sheeran – Home to You (Official Video 2025)]() 3:25
3:25
![Надежда Мельянцева - Котёнок, не плачь (Премьера клипа 2025)]() 3:02
3:02
![Alex Lim, Игорь Крутой - Вокзал (Премьера клипа 2025)]() 3:32
3:32
![Кравц - Пусть музыка играет (Премьера клипа 2025)]() 3:01
3:01
![NIKA DUBIK, Winter Spirit - Искры (Премьера клипа 2025)]() 4:27
4:27
![Абдуллах Борлаков, Мекка Борлакова - Звездная ночь (Премьера клипа 2025)]() 4:25
4:25
![Roza Zərgərli, Мурад Байкаев - Неизбежная любовь (Премьера клипа 2025)]() 2:34
2:34
![Слава - В сердце бьёт молния (Премьера клипа 2025)]() 3:30
3:30
![Азамат Ражабов - Нигорим (Премьера клипа 2025)]() 3:52
3:52
![Enrasta - За тобой (Премьера клипа 2025)]() 2:41
2:41
![Соня Белькевич, Олег Семенов - Увы, мадам (Премьера 2025)]() 3:33
3:33
![МАРАТ & АРНИ - Я ЖЕНИЛСЯ (Премьера клипа 2025)]() 4:16
4:16
![Tural Everest, Baarni - Ушедший покой (Премьера клипа 2025)]() 3:01
3:01
![Марина Хлебникова, Russell Ray - Солнышко (Премьера клипа 2025)]() 4:42
4:42
![Tamo ft Djan Edmonte - Ну что красавица (Премьера клипа 2025)]() 3:10
3:10
![Антон Макарский - Не уходи (Премьера клипа 2025)]() 3:41
3:41
![Руслан Шанов - Особенная (Премьера клипа 2025)]() 2:16
2:16
![Евгений Коновалов - Зачем ты меня целовала (Премьера клипа 2025)]() 3:17
3:17
![Иброхим Уткиров - Коракуз (Премьера клипа 2025)]() 4:28
4:28
![Властелин колец: Возвращение бомжа | The Lord of the Rings: The Return of the King (2003) (Гоблин)]() 3:21:07
3:21:07
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Рок-н-рольщик | RocknRolla (2008) (Гоблин)]() 1:54:23
1:54:23
![Святые из Бундока | The Boondock Saints (1999) (Гоблин)]() 1:48:30
1:48:30
![Большой куш / Спи#дили | Snatch (2000) (Гоблин)]() 1:42:50
1:42:50
![Отчаянный | Desperado (1995) (Гоблин)]() 1:40:18
1:40:18
![Однажды в Ирландии | The Guard (2011) (Гоблин)]() 1:32:16
1:32:16
![Гедда | Hedda (2025)]() 1:48:23
1:48:23
![Большое смелое красивое путешествие | A Big Bold Beautiful Journey (2025)]() 1:49:20
1:49:20
![Не грози Южному Централу, попивая сок у себя в квартале | Don't Be a Menace to South Central (1995) (Гоблин)]() 1:28:57
1:28:57
![Чумовая пятница 2 | Freakier Friday (2025)]() 1:50:38
1:50:38
![Большой Лебовски | The Big Lebowski (1998) (Гоблин)]() 1:56:59
1:56:59
![Властелин колец: Братва и кольцо | The Lord of the Rings: The Fellowship of the Ring (2001) ГОБЛИН]() 2:58:24
2:58:24
![Рука, качающая колыбель | The Hand That Rocks the Cradle (2025)]() 1:44:57
1:44:57
![Карты, деньги, два ствола | Lock, Stock and Two Smoking Barrels (1998) (Гоблин)]() 1:47:27
1:47:27
![Код 3 | Code 3 (2025)]() 1:39:56
1:39:56
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Свайпнуть | Swiped (2025)]() 1:50:35
1:50:35
![Трон: Арес | Tron: Ares (2025)]() 1:52:27
1:52:27
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Тодли Великолепный!]() 3:15
3:15
![Врумиз. 1 сезон]() 13:10
13:10
![Команда Дино Сезон 2]() 12:31
12:31
![МиниФорс]() 0:00
0:00
![Истории Баданаму Сезон 1]() 10:02
10:02
![Лудлвилль]() 7:09
7:09
![Умка]() 7:11
7:11
![Рэй и пожарный патруль Сезон 1]() 13:27
13:27
![Команда Дино Сезон 1]() 12:08
12:08
![Псэмми. Пять детей и волшебство Сезон 1]() 12:17
12:17
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Котёнок Шмяк]() 11:04
11:04
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Зомби Дамб]() 5:14
5:14
![Корги по имени Моко. Домашние животные]() 1:13
1:13
![Чемпионы]() 7:35
7:35
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Сборники «Зебра в клеточку»]() 45:30
45:30

 1:14:48
1:14:48Скачать видео
| 136x240 | ||
| 202x360 | ||
| 270x480 |
 4:44
4:44
2025-11-03 15:35
 3:25
3:25
2025-11-02 10:34
 3:02
3:02
2025-10-31 12:43
 3:32
3:32
2025-10-31 15:50
 3:01
3:01
2025-11-07 14:41
 4:27
4:27
2025-10-31 16:00
 4:25
4:25
2025-11-07 13:49
 2:34
2:34
2025-11-05 11:45
 3:30
3:30
2025-11-02 09:52
 3:52
3:52
2025-11-07 14:08
 2:41
2:41
2025-11-07 14:04
 3:33
3:33
2025-11-07 15:10
 4:16
4:16
2025-11-06 13:11
 3:01
3:01
2025-10-31 13:49
 4:42
4:42
2025-11-06 13:16
 3:10
3:10
2025-11-07 13:57
 3:41
3:41
2025-11-05 11:55
 2:16
2:16
2025-10-31 12:47
 3:17
3:17
2025-11-06 12:00
 4:28
4:28
2025-11-03 15:38
0/0
 3:21:07
3:21:07
2025-09-23 22:52
 2:02:20
2:02:20
2025-10-01 12:06
 1:54:23
1:54:23
2025-09-23 22:53
 1:48:30
1:48:30
2025-09-23 22:53
 1:42:50
1:42:50
2025-09-23 22:53
 1:40:18
1:40:18
2025-09-23 22:53
 1:32:16
1:32:16
2025-09-23 22:53
 1:48:23
1:48:23
2025-11-05 19:47
 1:49:20
1:49:20
2025-10-21 22:50
 1:28:57
1:28:57
2025-09-23 22:52
 1:50:38
1:50:38
2025-10-16 16:08
 1:56:59
1:56:59
2025-09-23 22:53
 2:58:24
2:58:24
2025-09-23 22:52
 1:44:57
1:44:57
2025-10-29 16:30
 1:47:27
1:47:27
2025-09-23 22:52
 1:39:56
1:39:56
2025-10-02 20:46
 2:15:54
2:15:54
2025-10-13 19:02
 2:09:55
2:09:55
2025-10-05 00:32
 1:50:35
1:50:35
2025-09-24 10:48
 1:52:27
1:52:27
2025-11-06 18:12
0/0
2021-09-22 22:45
 3:15
3:15
2025-06-10 13:56
2021-09-24 16:00
2021-09-22 22:40
 0:00
0:00
2025-11-08 03:28
2021-09-22 21:29
 7:09
7:09
2023-07-06 19:20
 7:11
7:11
2025-01-13 11:05
2021-09-22 23:51
2021-09-22 22:29
2021-09-22 22:23
2021-09-22 23:36
 11:04
11:04
2023-05-18 16:41
 6:30
6:30
2018-04-03 10:35
2021-09-22 21:49
 5:14
5:14
2024-11-28 13:12
 1:13
1:13
2024-11-29 14:40
 7:35
7:35
2025-11-01 09:00
2021-09-22 20:39
 45:30
45:30
2025-09-17 18:49
0/0

