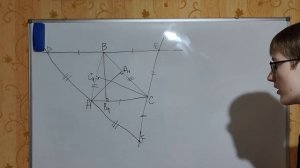
 4:16
4:16
2023-12-28 15:14

 10:04
10:04

 10:04
10:04
2025-09-08 20:04

 6:27
6:27

 6:27
6:27
2023-12-10 16:49

 2:15
2:15

 2:15
2:15
2025-09-25 22:19
 26:27
26:27

 26:27
26:27
2023-11-17 21:17

 4:53
4:53

 4:53
4:53
2023-12-06 10:20

 39:45
39:45

 39:45
39:45
2024-10-01 23:50

 2:18
2:18

 2:18
2:18
2024-04-11 12:33

 3:12
3:12

 3:12
3:12
2024-04-03 11:17

 8:42
8:42

 8:42
8:42
2024-02-09 10:44

 3:33
3:33

 3:33
3:33
2024-04-18 22:50

 12:34
12:34

 12:34
12:34
2023-10-07 12:40

 3:01
3:01

 3:01
3:01
2023-08-27 19:45

 27:23
27:23

 27:23
27:23
2023-07-09 17:32

 3:44
3:44

 3:44
3:44
2024-01-26 17:49

 1:37
1:37

 1:37
1:37
2023-08-19 18:41

 29:47
29:47

 29:47
29:47
2023-11-24 20:26
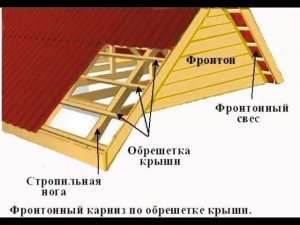
 1:22
1:22
![Бьянка - Бренд (Премьера клипа 2025)]() 2:29
2:29
![Фаррух Хамраев - Отажоним булсайди (Премьера клипа 2025)]() 3:08
3:08
![Азиз Абдуллох - Аллохнинг айтгани булади (Премьера клипа 2025)]() 3:40
3:40
![Шерзодбек Жонибеков - Дадажон (Премьера клипа 2025)]() 3:02
3:02
![Сергей Сухачёв - Розовый туман (Премьера клипа 2025)]() 3:13
3:13
![MILEN - Украду тебя (Премьера 2025)]() 3:40
3:40
![Дана Лахова - Одинокая луна (Премьера клипа 2025)]() 2:15
2:15
![Бонухон & Сардорбек Машарипов - Шанс (Премьера клипа 2025)]() 3:28
3:28
![Жалолиддин Ахмадалиев - Тонг отгунча (Премьера клипа 2025)]() 4:44
4:44
![Игорь Крутой - Зонтик (Премьера клипа 2025)]() 4:00
4:00
![SERYABKINA, Брутто - Светофоры (Премьера клипа 2025)]() 3:49
3:49
![Фати Царикаева - Стамбул (Премьера клипа 2025)]() 2:57
2:57
![Руслан Гасанов, Роман Ткаченко - Друзьям (Премьера клипа 2025)]() 3:20
3:20
![Magas - Без тебя (Премьера клипа 2025)]() 2:28
2:28
![MEDNA - Алё (Премьера клипа 2025)]() 2:28
2:28
![ИЮЛА - Ты был прав (Премьера клипа 2025)]() 2:21
2:21
![Анна Бершадская - Новая я (Премьера клипа 2025)]() 2:41
2:41
![Динара Швец - Новая история (Премьера клипа 2025)]() 3:45
3:45
![Олег Семенов - Бархатный сезон (Премьера клипа 2025)]() 3:51
3:51
![Виктория Качур - Одного тебя люблю (Премьера клипа 2025)]() 3:59
3:59
![Свинья | Pig (2021)]() 1:31:23
1:31:23
![Диспетчер | Relay (2025)]() 1:51:56
1:51:56
![Большое смелое красивое путешествие | A Big Bold Beautiful Journey (2025)]() 1:49:20
1:49:20
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Одноклассницы | St. Trinian's (2007)]() 1:36:32
1:36:32
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Богомол | Samagwi (2025)]() 1:53:29
1:53:29
![Храброе сердце | Braveheart (1995)]() 2:57:46
2:57:46
![Супруги Роуз | The Roses (2025)]() 1:45:29
1:45:29
![Государственный гимн | Americana (2025)]() 1:47:31
1:47:31
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![Непрощённая | The Unforgivable (2021)]() 1:54:10
1:54:10
![Псы войны | Hounds of War (2024)]() 1:34:38
1:34:38
![Свинтусы | The Twits (2025)]() 1:42:50
1:42:50
![Голос любви | Aline (2020)]() 2:05:43
2:05:43
![Молода и прекрасна | Jeune & jolie (2013)]() 1:33:24
1:33:24
![Чумовая пятница 2 | Freakier Friday (2025)]() 1:50:38
1:50:38
![Порочный круг | Vicious (2025)]() 1:42:30
1:42:30
![Голый пистолет | The Naked Gun (2025)]() 1:26:24
1:26:24
![Енотки]() 7:04
7:04
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Умка]() 7:11
7:11
![Таинственные золотые города]() 23:04
23:04
![Пакман в мире привидений]() 21:37
21:37
![Простоквашино]() 6:48
6:48
![Тодли Великолепный!]() 3:15
3:15
![МиниФорс Сезон 1]() 13:12
13:12
![Мотофайтеры]() 13:10
13:10
![Люк - путешественник во времени]() 1:19:50
1:19:50
![Псэмми. Пять детей и волшебство Сезон 1]() 12:17
12:17
![Лудлвилль]() 7:09
7:09
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Отряд А. Игрушки-спасатели]() 13:06
13:06
![Мартышкины]() 7:09
7:09
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Рэй и пожарный патруль Сезон 1]() 13:27
13:27
![Сборники «Ну, погоди!»]() 1:10:01
1:10:01
![МиниФорс]() 0:00
0:00
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:21
10:21

 1:22
1:22Скачать видео
| 256x144 | ||
| 426x240 | ||
| 640x360 | ||
| 854x480 | ||
| 1280x720 | ||
| 1920x1080 |
 2:29
2:29
2025-10-25 12:48
 3:08
3:08
2025-10-18 10:28
 3:40
3:40
2025-10-18 10:34
 3:02
3:02
2025-10-25 13:03
 3:13
3:13
2025-10-24 12:18
 3:40
3:40
2025-10-15 11:15
 2:15
2:15
2025-10-22 14:16
 3:28
3:28
2025-10-24 11:20
 4:44
4:44
2025-10-19 10:46
 4:00
4:00
2025-10-18 10:19
 3:49
3:49
2025-10-25 12:52
 2:57
2:57
2025-10-15 10:54
 3:20
3:20
2025-10-25 12:59
 2:28
2:28
2025-10-17 12:00
 2:28
2:28
2025-10-21 09:22
 2:21
2:21
2025-10-18 10:16
 2:41
2:41
2025-10-22 14:02
 3:45
3:45
2025-10-15 10:45
 3:51
3:51
2025-10-16 10:57
 3:59
3:59
2025-10-24 12:00
0/0
 1:31:23
1:31:23
2025-08-27 18:01
 1:51:56
1:51:56
2025-09-24 11:35
 1:49:20
1:49:20
2025-10-21 22:50
 2:09:55
2:09:55
2025-10-05 00:32
 1:36:32
1:36:32
2025-08-28 15:32
 1:35:11
1:35:11
2025-10-13 12:06
 2:15:54
2:15:54
2025-10-13 19:02
 1:53:29
1:53:29
2025-10-01 12:06
 2:57:46
2:57:46
2025-08-31 01:03
 1:45:29
1:45:29
2025-10-23 18:26
 1:47:31
1:47:31
2025-09-17 22:22
 1:29:27
1:29:27
2025-09-07 22:44
 1:54:10
1:54:10
2025-08-27 17:17
 1:34:38
1:34:38
2025-08-28 15:32
 1:42:50
1:42:50
2025-10-21 16:19
 2:05:43
2:05:43
2025-08-27 18:01
 1:33:24
1:33:24
2025-09-19 15:12
 1:50:38
1:50:38
2025-10-16 16:08
 1:42:30
1:42:30
2025-10-14 20:27
 1:26:24
1:26:24
2025-09-03 13:20
0/0
 7:04
7:04
2022-03-29 18:22
2021-09-22 21:03
 7:11
7:11
2025-01-13 11:05
 23:04
23:04
2025-01-09 17:26
 21:37
21:37
2024-11-28 17:35
 6:48
6:48
2025-10-17 10:00
 3:15
3:15
2025-06-10 13:56
2021-09-23 00:15
 13:10
13:10
2024-11-27 14:57
 1:19:50
1:19:50
2024-12-17 16:00
2021-09-22 22:23
 7:09
7:09
2023-07-06 19:20
 4:33
4:33
2024-12-17 16:56
 13:06
13:06
2024-11-28 16:30
 7:09
7:09
2025-04-01 16:06
2021-09-22 23:36
2021-09-22 23:51
 1:10:01
1:10:01
2025-07-25 20:16
 0:00
0:00
2025-10-26 16:00
 10:21
10:21
2025-09-11 10:05
0/0

