 3:22
3:22
2021-04-06 12:21

 14:47
14:47

 14:47
14:47
2024-11-11 02:04
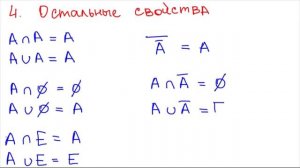
 12:10
12:10

 12:10
12:10
2023-12-03 01:07

 7:30
7:30

 7:30
7:30
2024-09-10 11:52

 7:16
7:16

 7:16
7:16
2023-12-02 07:10

 3:50
3:50

 3:50
3:50
2023-12-02 15:19

 17:18
17:18

 17:18
17:18
2023-12-30 04:20

 8:02
8:02

 8:02
8:02
2025-08-20 15:40

 11:51:08
11:51:08

 11:51:08
11:51:08
2025-12-05 07:23

 15:57
15:57

 15:57
15:57
2025-12-10 16:50

 1:26:07
1:26:07

 1:26:07
1:26:07
2025-12-09 11:00

 2:26:41
2:26:41

 2:26:41
2:26:41
2025-12-10 14:03

 3:15
3:15

 3:15
3:15
2025-08-21 18:39

 1:56:03
1:56:03

 1:56:03
1:56:03
2025-12-10 18:00

 4:33:45
4:33:45

 4:33:45
4:33:45
2025-12-10 19:25

 2:40:56
2:40:56

 2:40:56
2:40:56
2023-09-10 18:55

 50:47
50:47

 50:47
50:47
2025-12-10 19:00

 2:37:06
2:37:06
![Пропаганда - Дождь по крышам (Премьера 2025)]() 2:03
2:03
![Зардияна - Севган бахтли буларму (Премьера клипа 2025)]() 3:28
3:28
![Антон и Альфия - Ойся, ты ойся (Премьера клипа 2025)]() 3:04
3:04
![MIRAVI - Земля (Премьера клипа 2025)]() 2:26
2:26
![Tural Everest - Любить не хочет (Премьера клипа 2025)]() 2:55
2:55
![Отабек Холматов - Хамманинг уз дарди бор (Премьера клипа 2025)]() 3:10
3:10
![Камилла - Не плачь, девчонка (Премьера клипа 2025)]() 3:10
3:10
![Вадим Кузема - Осень-смешная пора (Премьера клипа 2025)]() 2:37
2:37
![BEST guruhi - Yana kim bor (Official Video 2025)]() 3:22
3:22
![Инна Вальтер - Не проиграть себе (Премьера клипа 2025)]() 3:04
3:04
![FEDUK - Ты была рядом (Премьера клипа 2025)]() 4:18
4:18
![Ahmed Shad - Афродита (Премьера клипа 2025)]() 2:57
2:57
![Оксана Джелиева - Курортный роман (Премьера клипа 2025)]() 2:45
2:45
![NAIMAN - Хулиганка (Премьера клипа 2025)]() 2:26
2:26
![Одилхужа Нодиров - Бегонадек (Премьера клипа 2025)]() 4:07
4:07
![Артур Бесаев - Все пройдет (Премьера клипа 2025)]() 3:44
3:44
![Ислам Итляшев - Пантера (Премьера клипа 2025)]() 3:07
3:07
![140 ударов в минуту – Мне тебя так мало (Премьера клипа 2025)]() 3:44
3:44
![Сергей Завьялов - Ты слёз своих не лей (Премьера 2025)]() 2:42
2:42
![Руслан Шанов - А если сердце так упрямится (Премьера клипа 2025)]() 3:36
3:36
![Код 3 | Code 3 (2025)]() 1:39:56
1:39:56
![Супруги Роуз | The Roses (2025)]() 1:45:29
1:45:29
![Paзpушитeль миpoв | Worldbreaker (2025)]() 1:34:45
1:34:45
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Бугония | Bugonia (2025)]() 1:59:12
1:59:12
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Боже. Как. Смешно. | Oh. What. Fun. (2025)]() 1:47:58
1:47:58
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Джей Келли | Jay Kelly (2025)]() 2:13:54
2:13:54
![Терминатор 2: Судный день | Terminator 2: Judgment Day (1991) (Гоблин)]() 2:36:13
2:36:13
![Только во сне | In Your Dreams (2025)]() 1:31:16
1:31:16
![Большое смелое красивое путешествие | A Big Bold Beautiful Journey (2025)]() 1:49:20
1:49:20
![Рука, качающая колыбель | The Hand That Rocks the Cradle (2025)]() 1:44:57
1:44:57
![Вальсируя с Брандо | Waltzing with Brando (2024)]() 1:44:15
1:44:15
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Крысы: Ведьмачья история | The Rats: A Witcher Tale (2025)]() 1:23:01
1:23:01
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Безжалостная | Stone Cold Fox (2025)]() 1:25:31
1:25:31
![Богомол | Samagwi (2025)]() 1:53:29
1:53:29
![Протокол выхода | Exit Protocol (2025)]() 1:24:45
1:24:45
![Приключения Пети и Волка]() 11:00
11:00
![Приключения Тайо]() 12:50
12:50
![Мотофайтеры]() 13:10
13:10
![Истории Баданаму Сезон 1]() 10:02
10:02
![Хвостатые песенки]() 7:00
7:00
![Енотки]() 7:04
7:04
![Сборники «Приключения Пети и Волка»]() 1:50:38
1:50:38
![Зебра в клеточку]() 6:30
6:30
![Минифорс. Сила динозавров]() 12:51
12:51
![Простоквашино. Финансовая грамотность]() 3:27
3:27
![Сборники «Ну, погоди!»]() 1:10:01
1:10:01
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:46
10:46
![Сборники «Умка»]() 1:20:52
1:20:52
![Чемпионы]() 7:15
7:15
![Корги по имени Моко. Волшебный мир снов]() 8:60
8:60
![Папа Супергерой Сезон 1]() 4:28
4:28
![Команда Дино Сезон 2]() 12:31
12:31
![Супер Дино]() 12:41
12:41
![Монсики]() 6:30
6:30
![Таинственные золотые города]() 23:04
23:04

 2:37:06
2:37:06Скачать Видео с Рутуба / RuTube
| 640x360 |
 2:03
2:03
2025-12-05 14:48
 3:28
3:28
2025-12-04 12:09
 3:04
3:04
2025-12-08 19:50
 2:26
2:26
2025-11-29 13:37
 2:55
2:55
2025-12-05 14:44
 3:10
3:10
2025-11-27 12:58
 3:10
3:10
2025-11-27 12:41
 2:37
2:37
2025-12-06 15:40
 3:22
3:22
2025-12-06 15:34
 3:04
3:04
2025-12-10 00:16
 4:18
4:18
2025-11-27 12:25
 2:57
2:57
2025-11-27 11:50
 2:45
2:45
2025-11-27 12:36
 2:26
2:26
2025-12-09 13:27
 4:07
4:07
2025-11-27 12:54
 3:44
3:44
2025-12-10 00:19
 3:07
3:07
2025-11-29 13:34
 3:44
3:44
2025-12-10 12:30
 2:42
2:42
2025-12-09 12:05
 3:36
3:36
2025-12-04 12:06
0/0
 1:39:56
1:39:56
2025-10-02 20:46
 1:45:29
1:45:29
2025-10-23 18:26
 1:34:45
1:34:45
2025-11-27 19:40
 1:47:25
1:47:25
2025-11-27 03:58
 1:59:12
1:59:12
2025-11-29 02:45
 1:35:11
1:35:11
2025-10-13 12:06
 1:47:58
1:47:58
2025-12-09 13:32
 2:32:29
2:32:29
2025-11-17 11:22
 2:13:54
2:13:54
2025-12-08 13:26
 2:36:13
2:36:13
2025-10-07 09:27
 1:31:16
1:31:16
2025-11-21 20:18
 1:49:20
1:49:20
2025-10-21 22:50
 1:44:57
1:44:57
2025-10-29 16:30
 1:44:15
1:44:15
2025-11-07 20:19
 1:18:55
1:18:55
2025-11-21 14:16
 1:23:01
1:23:01
2025-11-05 19:47
 2:02:20
2:02:20
2025-10-01 12:06
 1:25:31
1:25:31
2025-11-10 21:11
 1:53:29
1:53:29
2025-10-01 12:06
 1:24:45
1:24:45
2025-11-13 23:26
0/0
 11:00
11:00
2022-04-01 17:59
 12:50
12:50
2024-12-17 13:25
 13:10
13:10
2024-11-27 14:57
2021-09-22 21:29
 7:00
7:00
2025-06-01 11:15
 7:04
7:04
2022-03-29 18:22
 1:50:38
1:50:38
2025-10-29 16:37
 6:30
6:30
2022-03-31 13:09
 12:51
12:51
2024-11-27 16:39
 3:27
3:27
2024-12-07 11:00
 1:10:01
1:10:01
2025-07-25 20:16
 10:46
10:46
2022-06-07 11:02
 1:20:52
1:20:52
2025-09-19 17:54
 7:15
7:15
2025-12-10 10:00
 8:60
8:60
2025-12-09 11:58
2021-09-22 21:52
2021-09-22 22:40
 12:41
12:41
2024-11-28 12:54
 6:30
6:30
2022-03-29 19:16
 23:04
23:04
2025-01-09 17:26
0/0

