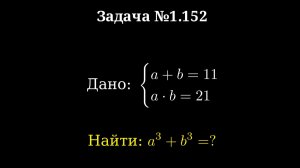
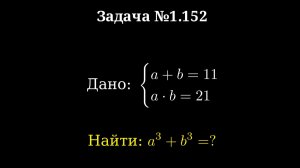 2:54
2:54
2025-11-24 17:43

 3:50
3:50

 3:50
3:50
2025-11-27 19:44
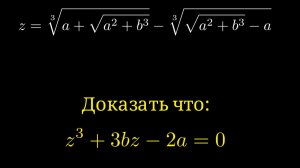
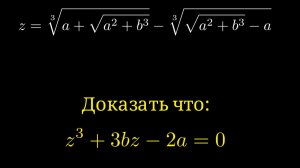 4:49
4:49
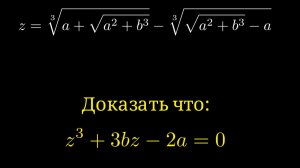
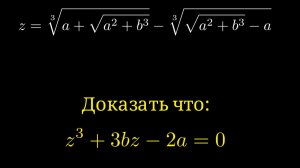 4:49
4:49
2025-11-27 11:33

 22:13
22:13

 22:13
22:13
2025-11-28 08:00

 2:11:51
2:11:51

 2:11:51
2:11:51
2025-11-28 12:01

 3:15
3:15

 3:15
3:15
2024-09-23 12:30

 6:19
6:19

 6:19
6:19
2025-06-22 13:28

 3:22
3:22

 3:22
3:22
2025-01-03 22:31

 1:56:29
1:56:29

 1:56:29
1:56:29
2025-11-15 21:00

 1:54:53
1:54:53

 1:54:53
1:54:53
2025-11-28 21:50

 3:00:33
3:00:33

 3:00:33
3:00:33
2025-11-29 19:57

 1:39:05
1:39:05

 1:39:05
1:39:05
2025-11-28 00:01

 1:05:25
1:05:25

 1:05:25
1:05:25
2025-11-29 18:09

 1:11:18
1:11:18

 1:11:18
1:11:18
2025-11-27 09:37

 2:40:56
2:40:56

 2:40:56
2:40:56
2023-09-10 18:55

 3:48:10
3:48:10

 3:48:10
3:48:10
2023-09-18 01:16

 48:30
48:30

 48:30
48:30
2025-11-29 18:55

 46:08
46:08
![Шамиль Кашешов - Когда мы встретились с тобой (Премьера клипа 2025)]() 3:10
3:10
![Зульфия Чотчаева - Холодное сердце (Премьера клипа 2025)]() 2:52
2:52
![Алмас Багратиони - Дети света (Премьера клипа 2025)]() 2:52
2:52
![SHODI - Не верь, не бойся, не проси]() 2:49
2:49
![Отабек Муминов - Кетябсан (Премьера клипа 2025)]() 3:17
3:17
![Ахрор Гуломов - Ёмгирлар (Премьера клипа 2025)]() 3:49
3:49
![FEDUK - Ты была рядом (Премьера клипа 2025)]() 4:18
4:18
![Хушнуд - Бевафо ёр (Премьера клипа 2025)]() 5:39
5:39
![Рейсан Магомедкеримов - Моя мадам (Премьера клипа 2025)]() 3:28
3:28
![NAIMAN - Плакала (Премьера клипа 2025)]() 2:21
2:21
![Ислам Итляшев - Не реви (Премьера клипа 2025)]() 2:41
2:41
![Мужик из СИБИРИ (Александр Конев) - Поцелуи осени (Премьера клипа 2025)]() 2:59
2:59
![Бунёд Бобокулов - Отам-онам (Премьера клипа 2025)]() 4:00
4:00
![ZIMMA - Город Тает (Премьера клипа 2025)]() 2:30
2:30
![RRuslan - Снова ночь (Премьера клипа 2025)]() 3:05
3:05
![Шавкат Зулфикор & Нурзида Исаева - Одамнинг ёмони ёмон буларкан (Премьера клипа 2025)]() 8:21
8:21
![Шохжахон Раҳмиддинов - Арзон (Премьера клипа 2025)]() 3:40
3:40
![Cvetocek7 - Голос твой (Премьера клипа 2025)]() 2:44
2:44
![Азамат Исенгазин - Мой свет (Премьера 2025)]() 2:47
2:47
![Катя Маркеданец - Мама (Премьера клипа 2025)]() 3:32
3:32
![Сны поездов | Train Dreams (2025)]() 1:43:45
1:43:45
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Большой Лебовски | The Big Lebowski (1998) (Гоблин)]() 1:56:59
1:56:59
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Плохой Cанта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:28:32
1:28:32
![Бешеные псы | Reservoir Dogs (1991) (Гоблин)]() 1:39:10
1:39:10
![Тот самый | Him (2025)]() 1:36:20
1:36:20
![Битва за битвой | One Battle After Another (2025)]() 2:41:45
2:41:45
![Стив | Steve (2025)]() 1:33:34
1:33:34
![Супергеройское кино | Superhero Movie (2008)]() 1:22:33
1:22:33
![Орудия | Weapons (2025)]() 2:08:34
2:08:34
![Хищник | Predator (1987) (Гоблин)]() 1:46:40
1:46:40
![Свинтусы | The Twits (2025)]() 1:42:50
1:42:50
![Только ты | All of You (2025)]() 1:38:22
1:38:22
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Цельнометаллическая оболочка | Full Metal Jacket (1987) (Гоблин)]() 1:56:34
1:56:34
![Баллада о маленьком игроке | Ballad of a Small Player (2025)]() 1:42:60
1:42:60
![Только во сне | In Your Dreams (2025)]() 1:31:16
1:31:16
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Трон: Арес | Tron: Ares (2025)]() 1:52:27
1:52:27
![Псэмми. Пять детей и волшебство Сезон 1]() 12:17
12:17
![Тайны Медовой долины]() 7:01
7:01
![Зомби Дамб]() 5:14
5:14
![Врумиз. 1 сезон]() 13:10
13:10
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![Монсики]() 6:30
6:30
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Сборники «Приключения Пети и Волка»]() 1:50:38
1:50:38
![Сборники «Умка»]() 1:20:52
1:20:52
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Корги по имени Моко. Домашние животные]() 1:13
1:13
![Котёнок Шмяк]() 11:04
11:04
![Хвостатые песенки]() 7:00
7:00
![Пип и Альба Сезон 1]() 11:02
11:02
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Люк - путешественник во времени]() 1:19:50
1:19:50
![Пиратская школа]() 11:06
11:06
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24
![Мотофайтеры]() 13:10
13:10
![Кадеты Баданаму Сезон 1]() 11:50
11:50

 46:08
46:08Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 3:10
3:10
2025-11-22 12:41
 2:52
2:52
2025-11-18 11:48
 2:52
2:52
2025-11-20 13:43
 2:49
2:49
2025-11-26 14:57
 3:17
3:17
2025-11-15 12:47
 3:49
3:49
2025-11-15 12:54
 4:18
4:18
2025-11-27 12:25
 5:39
5:39
2025-11-23 13:40
 3:28
3:28
2025-11-20 13:54
 2:21
2:21
2025-11-18 12:25
 2:41
2:41
2025-11-18 12:35
 2:59
2:59
2025-11-21 13:10
 4:00
4:00
2025-11-21 13:29
 2:30
2:30
2025-11-21 13:20
 3:05
3:05
2025-11-25 11:19
 8:21
8:21
2025-11-17 14:27
 3:40
3:40
2025-11-21 13:31
 2:44
2:44
2025-11-26 14:25
 2:47
2:47
2025-11-19 11:44
 3:32
3:32
2025-11-17 14:20
0/0
 1:43:45
1:43:45
2025-11-26 14:01
 1:46:45
1:46:45
2025-10-02 20:45
 1:56:59
1:56:59
2025-09-23 22:53
 1:35:11
1:35:11
2025-10-13 12:06
 1:28:32
1:28:32
2025-10-07 09:27
 1:39:10
1:39:10
2025-09-23 22:53
 1:36:20
1:36:20
2025-10-09 20:02
 2:41:45
2:41:45
2025-11-14 13:17
 1:33:34
1:33:34
2025-10-08 12:27
 1:22:33
1:22:33
2025-11-21 14:16
 2:08:34
2:08:34
2025-09-24 22:05
 1:46:40
1:46:40
2025-10-07 09:27
 1:42:50
1:42:50
2025-10-21 16:19
 1:38:22
1:38:22
2025-10-01 12:16
 2:15:54
2:15:54
2025-10-13 19:02
 1:56:34
1:56:34
2025-09-23 22:53
 1:42:60
1:42:60
2025-10-31 10:53
 1:31:16
1:31:16
2025-11-21 20:18
 2:32:29
2:32:29
2025-11-17 11:22
 1:52:27
1:52:27
2025-11-06 18:12
0/0
2021-09-22 22:23
 7:01
7:01
2022-03-30 17:25
 5:14
5:14
2024-11-28 13:12
2021-09-24 16:00
 6:30
6:30
2018-04-03 10:35
 6:30
6:30
2022-03-29 19:16
 13:00
13:00
2024-11-28 16:19
 1:50:38
1:50:38
2025-10-29 16:37
 1:20:52
1:20:52
2025-09-19 17:54
2021-09-22 21:49
 1:13
1:13
2024-11-29 14:40
 11:04
11:04
2023-05-18 16:41
 7:00
7:00
2025-06-01 11:15
2021-09-22 23:37
 3:28
3:28
2025-01-09 17:01
 1:19:50
1:19:50
2024-12-17 16:00
 11:06
11:06
2022-04-01 15:56
 12:24
12:24
2024-11-27 13:24
 13:10
13:10
2024-11-27 14:57
2021-09-22 21:17
0/0

