 4:22
4:22
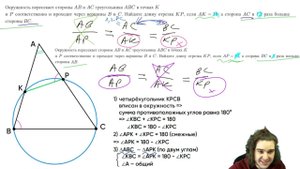
ОТВЕТ В ОДНО ДЕЙСТВИЕ. Окружность пересекает стороны треугольника в точках и проходит через вершины.
2024-04-16 13:00

 8:02
8:02

 8:02
8:02
2024-10-21 10:19

 1:13
1:13

 1:13
1:13
2025-09-25 18:03

 32:16
32:16

 32:16
32:16
2025-09-20 09:34

 1:55:45
1:55:45

 1:55:45
1:55:45
2025-09-16 20:14

 10:29
10:29

 10:29
10:29
2025-09-22 09:39

 5:30
5:30

 5:30
5:30
2025-09-24 07:00

 7:40
7:40

 7:40
7:40
2025-09-25 17:00

 1:23:24
1:23:24

 1:23:24
1:23:24
2025-09-18 12:00

 2:14
2:14

 2:14
2:14
2025-09-19 15:42

 1:06:32
1:06:32

 1:06:32
1:06:32
2025-09-16 12:56

 1:50:16
1:50:16

 1:50:16
1:50:16
2025-09-15 14:19

 6:00
6:00

 6:00
6:00
2025-09-27 16:00

 19:12
19:12

 19:12
19:12
2025-09-11 14:41

 7:19
7:19

 7:19
7:19
2025-09-24 15:35

 3:20
3:20

 3:20
3:20
2025-09-11 10:37

 24:23
24:23

 24:23
24:23
2025-09-11 09:20
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14
![ARTEE - Лети (Премьера клипа 2025)]() 3:13
3:13
![Сардор Расулов - Етолмадим (Премьера клипа 2025)]() 4:15
4:15
![5sta Family - Антидот (Премьера клипа 2025)]() 3:33
3:33
![Зара - Я несла свою беду (Премьера клипа 2025)]() 3:36
3:36
![Рейсан Магомедкеримов, Ренат Омаров - Бла-та-та (Премьера клипа 2025)]() 2:26
2:26
![Ислам Итляшев - Не вспоминай (Премьера клипа 2025)]() 2:52
2:52
![MEDNA - Алё (Премьера клипа 2025)]() 2:28
2:28
![Игорь Крутой - Зонтик (Премьера клипа 2025)]() 4:00
4:00
![ИЮЛА - Ты был прав (Премьера клипа 2025)]() 2:21
2:21
![INSTASAMKA - BOSS (Премьера клипа 2025)]() 3:41
3:41
![Taylor Swift - The Fate of Ophelia (Official Video 2025)]() 3:58
3:58
![МАРАТ & АРНИ - Стала женой (Премьера клипа 2025)]() 3:51
3:51
![Zhamil Turan - Капали (Премьера клипа 2025)]() 3:08
3:08
![Гор Мартиросян - 101 роза (Премьера клипа 2025)]() 4:26
4:26
![Ольга Бузова - Не надо (Премьера клипа 2025)]() 3:15
3:15
![MARSO - Дура (Премьера клипа 2025)]() 3:05
3:05
![Светлана Ларионова - Осень отстой (Премьера клипа 2025)]() 3:30
3:30
![Джатдай - Забери печаль (Премьера клипа 2025)]() 2:29
2:29
![Selena Gomez - In The Dark (Official Video 2025)]() 3:04
3:04
![Дана Лахова - Одинокая луна (Премьера клипа 2025)]() 2:15
2:15
![Вечеринка только начинается | The Party's Just Beginning (2018)]() 1:31:20
1:31:20
![Одноклассницы | St. Trinian's (2007)]() 1:36:32
1:36:32
![Диспетчер | Relay (2025)]() 1:51:56
1:51:56
![F1 (2025)]() 2:35:53
2:35:53
![Сверху вниз | Highest 2 Lowest (2025)]() 2:13:21
2:13:21
![Мальчишник в Таиланде | Changeland (2019)]() 1:25:47
1:25:47
![Сумерки | Twilight (2008)]() 2:01:55
2:01:55
![Счастливчик Гилмор 2 | Happy Gilmore (2025)]() 1:57:36
1:57:36
![Псы войны | Hounds of War (2024)]() 1:34:38
1:34:38
![Супруги Роуз | The Roses (2025)]() 1:45:29
1:45:29
![Только ты | All of You (2025)]() 1:38:22
1:38:22
![Свинья | Pig (2021)]() 1:31:23
1:31:23
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Лучшее Рождество! | Nativity! (2009)]() 1:46:00
1:46:00
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Обитель | The Home (2025)]() 1:34:43
1:34:43
![Мужчина у меня в подвале | The Man in My Basement (2025)]() 1:54:48
1:54:48
![Хани, не надо! | Honey Don't! (2025)]() 1:29:32
1:29:32
![Хвостатые песенки]() 7:00
7:00
![Школьный автобус Гордон]() 12:34
12:34
![Крутиксы]() 11:00
11:00
![Сборники «Приключения Пети и Волка»]() 1:50:35
1:50:35
![Оранжевая корова]() 6:30
6:30
![Простоквашино]() 6:48
6:48
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Мартышкины]() 7:09
7:09
![Полли Покет Сезон 1]() 21:30
21:30
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Зебра в клеточку]() 6:30
6:30
![Чуч-Мяуч]() 7:04
7:04
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Люк - путешественник во времени]() 1:19:50
1:19:50
![Папа Супергерой Сезон 1]() 4:28
4:28
![Сборники «Оранжевая корова»]() 1:05:15
1:05:15
![Тайны Медовой долины]() 7:01
7:01
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14Скачать видео
| 256x144 | ||
| 640x360 |
 3:13
3:13
2025-10-18 09:47
 4:15
4:15
2025-10-26 12:52
 3:33
3:33
2025-10-22 13:57
 3:36
3:36
2025-10-18 10:07
 2:26
2:26
2025-10-22 14:10
 2:52
2:52
2025-10-28 10:47
 2:28
2:28
2025-10-21 09:22
 4:00
4:00
2025-10-18 10:19
 2:21
2:21
2025-10-18 10:16
 3:41
3:41
2025-10-23 13:04
 3:58
3:58
2025-10-17 11:48
 3:51
3:51
2025-10-16 11:41
 3:08
3:08
2025-10-22 14:26
 4:26
4:26
2025-10-25 12:55
 3:15
3:15
2025-10-18 10:02
 3:05
3:05
2025-10-17 11:37
 3:30
3:30
2025-10-24 11:42
 2:29
2:29
2025-10-24 11:25
 3:04
3:04
2025-10-24 11:30
 2:15
2:15
2025-10-22 14:16
0/0
 1:31:20
1:31:20
2025-08-27 17:17
 1:36:32
1:36:32
2025-08-28 15:32
 1:51:56
1:51:56
2025-09-24 11:35
 2:35:53
2:35:53
2025-08-26 11:45
 2:13:21
2:13:21
2025-09-09 12:49
 1:25:47
1:25:47
2025-08-27 17:17
 2:01:55
2:01:55
2025-08-28 15:32
 1:57:36
1:57:36
2025-08-21 17:43
 1:34:38
1:34:38
2025-08-28 15:32
 1:45:29
1:45:29
2025-10-23 18:26
 1:38:22
1:38:22
2025-10-01 12:16
 1:31:23
1:31:23
2025-08-27 18:01
 2:02:20
2:02:20
2025-10-01 12:06
 1:54:40
1:54:40
2025-09-24 11:35
 1:46:00
1:46:00
2025-08-27 17:17
 1:29:27
1:29:27
2025-09-07 22:44
 2:15:54
2:15:54
2025-10-13 19:02
 1:34:43
1:34:43
2025-09-09 12:49
 1:54:48
1:54:48
2025-10-01 15:17
 1:29:32
1:29:32
2025-09-15 11:39
0/0
 7:00
7:00
2025-06-01 11:15
 12:34
12:34
2024-12-02 14:42
 11:00
11:00
2022-07-25 18:59
 1:50:35
1:50:35
2025-07-15 11:13
 6:30
6:30
2022-03-31 18:49
 6:48
6:48
2025-10-17 10:00
 3:28
3:28
2025-01-09 17:01
 6:30
6:30
2018-04-03 10:35
2021-09-22 21:03
 7:09
7:09
2025-04-01 16:06
2021-09-22 23:09
2021-09-22 20:39
 6:30
6:30
2022-03-31 13:09
 7:04
7:04
2022-03-29 15:20
 13:00
13:00
2024-11-28 16:19
 1:19:50
1:19:50
2024-12-17 16:00
2021-09-22 21:52
 1:05:15
1:05:15
2025-09-30 13:45
 7:01
7:01
2022-03-30 17:25
 4:33
4:33
2024-12-17 16:56
0/0

