 2:50
2:50
2025-01-28 06:55
 5:59
5:59

 5:59
5:59
2024-08-07 23:08

 5:07
5:07

 5:07
5:07
2024-11-27 09:30

 10:29
10:29

 10:29
10:29
2025-09-22 09:39
 4:59
4:59

 4:59
4:59
2024-08-08 16:28

 34:56
34:56

 34:56
34:56
2025-09-12 16:44

 1:06:32
1:06:32

 1:06:32
1:06:32
2025-09-16 12:56

 3:20
3:20

 3:20
3:20
2025-09-11 10:37

 1:23:24
1:23:24

 1:23:24
1:23:24
2025-09-18 12:00
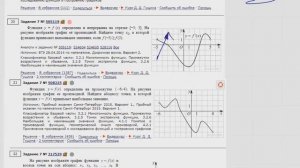
 1:25
1:25

 1:25
1:25
2023-12-28 14:32
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14
2025-09-23 12:00
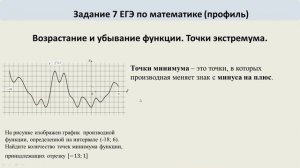
 1:44
1:44

 1:44
1:44
2022-04-01 11:52
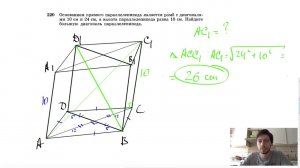
 2:29
2:29

 2:29
2:29
2020-02-04 14:48
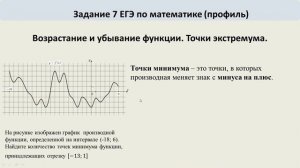
 1:44
1:44

 1:44
1:44
2023-09-14 20:12

 17:28
17:28

 17:28
17:28
2022-01-10 16:24

 2:42
2:42

 2:42
2:42
2022-11-10 06:10
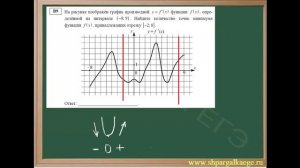
 2:49
2:49

 2:49
2:49
2023-09-10 15:21
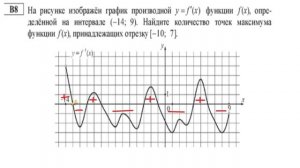
 2:01
2:01
![INSTASAMKA - AGENT GIRL (Премьера клипа 2025)]() 3:24
3:24
![Zhamil Turan - Капали (Премьера клипа 2025)]() 3:08
3:08
![ARTEE - Лети (Премьера клипа 2025)]() 3:13
3:13
![Taylor Swift - The Fate of Ophelia (Official Video 2025)]() 3:58
3:58
![5sta Family - Антидот (Премьера клипа 2025)]() 3:33
3:33
![Азамат Ражабов - Отам (Премьера клипа 2025)]() 4:38
4:38
![Игорь Крутой - Зонтик (Премьера клипа 2025)]() 4:00
4:00
![Рейсан Магомедкеримов - Забываю (Премьера клипа 2025)]() 3:20
3:20
![Фати Царикаева - Стамбул (Премьера клипа 2025)]() 2:57
2:57
![Наталья Влади - А я такая (Премьера клипа 2025)]() 2:21
2:21
![Рустам Батербиев - Пора расстаться (Премьера клипа 2025)]() 2:38
2:38
![Артур Пирожков - ALARM (Премьера клипа 2025)]() 3:22
3:22
![Ислам Итляшев - Скандал (Премьера клипа 2025)]() 2:08
2:08
![MEDNA - Алё (Премьера клипа 2025)]() 2:28
2:28
![Анна Бершадская - Новая я (Премьера клипа 2025)]() 2:41
2:41
![Анвар Нишонов - Тулкилар (Премьера клипа 2025)]() 3:38
3:38
![Олег Семенов - Бархатный сезон (Премьера клипа 2025)]() 3:51
3:51
![Толиб Тухтасинов - Хоп-Хоп (Премьера клипа 2025)]() 3:09
3:09
![Динара Швец - Новая история (Премьера клипа 2025)]() 3:45
3:45
![Зара - Я несла свою беду (Премьера клипа 2025)]() 3:36
3:36
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Бастион 36 | Bastion 36 (2025)]() 2:04:58
2:04:58
![M3GAN 2 | M3GAN 2.0 (2025)]() 2:00:03
2:00:03
![Милая вилла | La Dolce Villa (2025)]() 1:39:20
1:39:20
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Улица Страха: Королева выпускного | Fear Street: Prom Queen (2025)]() 1:30:05
1:30:05
![Моя мертвая подруга Зои | My Dead Friend Zoe (2024)]() 1:42:40
1:42:40
![Долина эха | Echo Valley (2025)]() 1:44:37
1:44:37
![Опустошение | Havoc (2025)]() 1:47:26
1:47:26
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Хани, не надо! | Honey Don't! (2025)]() 1:29:32
1:29:32
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![F1 (2025)]() 2:35:53
2:35:53
![Актер | The Actor (2025)]() 1:38:13
1:38:13
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Бабули | Nonnas (2025)]() 1:54:10
1:54:10
![Углубление (2025)]() 2:07:52
2:07:52
![Блиц | Blitz (2024)]() 2:00:30
2:00:30
![Обитель | The Home (2025)]() 1:34:43
1:34:43
![Кирпич | Brick]() 1:40:58
1:40:58
![Полли Покет Сезон 1]() 21:30
21:30
![Истории Баданаму Сезон 1]() 10:02
10:02
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Сборники «Зебра в клеточку»]() 45:30
45:30
![Люк - путешественник во времени]() 1:19:50
1:19:50
![Школьный автобус Гордон]() 12:34
12:34
![МиниФорс]() 0:00
0:00
![Шахерезада. Нерассказанные истории Сезон 1]() 23:53
23:53
![Зебра в клеточку]() 6:30
6:30
![Папа Супергерой Сезон 1]() 4:28
4:28
![Отважные мишки]() 13:00
13:00
![Тодли Великолепный!]() 3:15
3:15
![Космический рейнджер Роджер Сезон 1]() 11:32
11:32
![Забавные медвежата]() 13:00
13:00
![Новогодние мультики – Союзмультфильм]() 7:04
7:04
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Приключения Пети и Волка]() 11:00
11:00
![Пиратская школа]() 11:06
11:06
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:21
10:21
![Простоквашино. Финансовая грамотность]() 3:27
3:27

 2:01
2:01Скачать видео
| 256x144 | ||
| 640x360 | ||
| 1280x720 |
 3:24
3:24
2025-10-17 11:33
 3:08
3:08
2025-10-22 14:26
 3:13
3:13
2025-10-18 09:47
 3:58
3:58
2025-10-17 11:48
 3:33
3:33
2025-10-22 13:57
 4:38
4:38
2025-10-11 12:52
 4:00
4:00
2025-10-18 10:19
 3:20
3:20
2025-10-16 11:19
 2:57
2:57
2025-10-15 10:54
 2:21
2:21
2025-10-14 11:07
 2:38
2:38
2025-10-16 11:06
 3:22
3:22
2025-10-20 14:44
 2:08
2:08
2025-10-14 10:40
 2:28
2:28
2025-10-21 09:22
 2:41
2:41
2025-10-22 14:02
 3:38
3:38
2025-10-11 12:45
 3:51
3:51
2025-10-16 10:57
 3:09
3:09
2025-10-11 21:54
 3:45
3:45
2025-10-15 10:45
 3:36
3:36
2025-10-18 10:07
0/0
 1:35:11
1:35:11
2025-10-13 12:06
 2:04:58
2:04:58
2025-04-26 17:36
 2:00:03
2:00:03
2025-07-19 19:23
 1:39:20
1:39:20
2025-03-21 12:00
 2:15:54
2:15:54
2025-10-13 19:02
 1:30:05
1:30:05
2025-06-16 20:00
 1:42:40
1:42:40
2025-05-16 16:49
 1:44:37
1:44:37
2025-08-03 10:47
 1:47:26
1:47:26
2025-08-02 13:33
 1:46:45
1:46:45
2025-10-02 20:45
 1:29:32
1:29:32
2025-09-15 11:39
 1:29:27
1:29:27
2025-09-07 22:44
 2:35:53
2:35:53
2025-08-26 11:45
 1:38:13
1:38:13
2025-04-09 20:04
 2:02:20
2:02:20
2025-10-01 12:06
 1:54:10
1:54:10
2025-06-20 15:43
 2:07:52
2:07:52
2025-02-18 18:05
 2:00:30
2:00:30
2025-01-18 21:22
 1:34:43
1:34:43
2025-09-09 12:49
 1:40:58
1:40:58
2025-08-03 10:48
0/0
2021-09-22 23:09
2021-09-22 21:29
2021-09-22 23:36
 45:30
45:30
2025-09-17 18:49
 1:19:50
1:19:50
2024-12-17 16:00
 12:34
12:34
2024-12-02 14:42
 0:00
0:00
2025-10-23 13:57
2021-09-22 23:25
 6:30
6:30
2022-03-31 13:09
2021-09-22 21:52
 13:00
13:00
2024-11-29 13:39
 3:15
3:15
2025-06-10 13:56
2021-09-22 21:49
 13:00
13:00
2024-12-02 13:15
 7:04
7:04
2023-07-25 00:09
 3:28
3:28
2025-01-09 17:01
 11:00
11:00
2022-04-01 17:59
 11:06
11:06
2022-04-01 15:56
 10:21
10:21
2025-09-11 10:05
 3:27
3:27
2024-12-07 11:00
0/0