
 16:57
16:57
2025-03-02 16:05

 20:49
20:49

 20:49
20:49
2025-01-30 14:07

 29:22
29:22

 29:22
29:22
2023-12-17 09:53

 9:06
9:06

 9:06
9:06
2024-10-30 16:45

 21:09
21:09

 21:09
21:09
2024-03-28 09:25

 10:25
10:25

 10:25
10:25
2025-09-01 14:57

 10:19
10:19

 10:19
10:19
2025-09-01 13:42

 15:46
15:46

 15:46
15:46
2024-02-03 00:29

 2:06
2:06

 2:06
2:06
2024-04-25 11:46

 0:22
0:22

 0:22
0:22
2024-02-16 22:30

 25:08
25:08

 25:08
25:08
2024-03-31 09:43
![Применение производной для исследования функций на монотонность и экстремумы]() 9:29
9:29
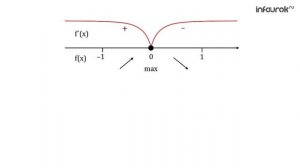 9:29
9:29
2021-03-19 16:45
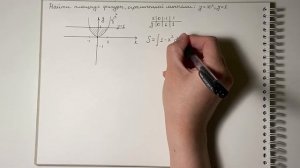
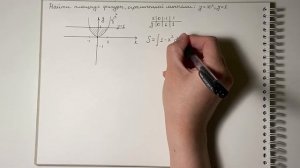 4:30
4:30
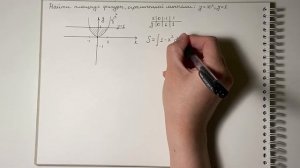
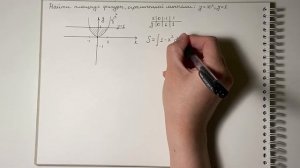 4:30
4:30
2023-09-30 19:06

 10:08
10:08

 10:08
10:08
2023-09-04 08:49

 6:49
6:49

 6:49
6:49
2023-08-04 10:37

 15:46
15:46

 15:46
15:46
2023-08-13 14:27
![МУВИК ПОД ЛУЧШИЙ ФОНК ❤️ [0.24.0]](https://pic.rutubelist.ru/video/3c/21/3c21c8392314bd80944d04cd27503ca8.jpg?width=300)
 0:53
0:53
![МУВИК ПОД ЛУЧШИЙ ФОНК ❤️ [0.24.0]](https://pic.rutubelist.ru/video/3c/21/3c21c8392314bd80944d04cd27503ca8.jpg?width=300)
 0:53
0:53
2023-08-17 20:25

 30:37
30:37
![Бекзод Хаккиев - Айтаман (Премьера клипа 2025)]() 2:41
2:41
![Зульфия Чотчаева - Холодное сердце (Премьера клипа 2025)]() 2:52
2:52
![Отабек Муминов - Кетябсан (Премьера клипа 2025)]() 3:17
3:17
![Zhamil Turan - Губки не целованы (Премьера клипа 2025)]() 2:37
2:37
![Ozoda - Chamadon (Official Video 2025)]() 5:23
5:23
![Enrasta - Франция (Премьера клипа 2025)]() 2:44
2:44
![ZIMMA - Город Тает (Премьера клипа 2025)]() 2:30
2:30
![Владимир Ждамиров, Игорь Кибирев - Тик так (Премьера 2025)]() 3:30
3:30
![KhaliF - Я розы тебе принес (Премьера клипа 2025)]() 2:06
2:06
![Соня Белькевич - Подогналась (Премьера клипа 2025)]() 3:13
3:13
![Ахрор Гуломов - Ёмгирлар (Премьера клипа 2025)]() 3:49
3:49
![Ольга Стельмах – Не будем всё усложнять (Премьера клипа 2025)]() 4:01
4:01
![POLAT - Лунная (Премьера клипа 2025)]() 2:34
2:34
![Даша Эпова - Мой любимый человек (Премьера клипа 2025)]() 2:11
2:11
![Женя Белоусова - Раненая птица (Премьера клипа 2025)]() 2:47
2:47
![Катя Маркеданец - Мама (Премьера клипа 2025)]() 3:32
3:32
![Рейсан Магомедкеримов - Моя мадам (Премьера клипа 2025)]() 3:28
3:28
![Азамат Исенгазин - Мой свет (Премьера 2025)]() 2:47
2:47
![SHAXO - Пьяница (Премьера клипа 2025)]() 3:32
3:32
![Эльдар Агачев - Путник (Премьера клипа 2025)]() 3:14
3:14
![Однажды в Ирландии | The Guard (2011) (Гоблин)]() 1:32:16
1:32:16
![Все дьяволы здесь | All the Devils are Here (2025)]() 1:31:39
1:31:39
![Отчаянный | Desperado (1995) (Гоблин)]() 1:40:18
1:40:18
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Супергеройское кино | Superhero Movie (2008)]() 1:22:33
1:22:33
![Плохой Санта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:34:55
1:34:55
![Стив | Steve (2025)]() 1:33:34
1:33:34
![Кей-поп-охотницы на демонов | KPop Demon Hunters (2025)]() 1:39:41
1:39:41
![Убойная суббота | Playdate (2025)]() 1:34:35
1:34:35
![Плохой Cанта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:28:32
1:28:32
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Бешеные псы | Reservoir Dogs (1991) (Гоблин)]() 1:39:10
1:39:10
![Большое смелое красивое путешествие | A Big Bold Beautiful Journey (2025)]() 1:49:20
1:49:20
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Хищник | Predator (1987) (Гоблин)]() 1:46:40
1:46:40
![Чёрный телефон 2 | Black Phone 2 (2025)]() 1:53:55
1:53:55
![Супруги Роуз | The Roses (2025)]() 1:45:29
1:45:29
![Крысы: Ведьмачья история | The Rats: A Witcher Tale (2025)]() 1:23:01
1:23:01
![Цельнометаллическая оболочка | Full Metal Jacket (1987) (Гоблин)]() 1:56:34
1:56:34
![Вальсируя с Брандо | Waltzing with Brando (2024)]() 1:44:15
1:44:15
![Врумиз. 1 сезон]() 13:10
13:10
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24
![Сборники «Оранжевая корова»]() 1:05:15
1:05:15
![Тодли Великолепный!]() 3:15
3:15
![МегаМен: Полный заряд Сезон 1]() 10:42
10:42
![Артур и дети круглого стола]() 11:22
11:22
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![МиниФорс Сезон 1]() 13:12
13:12
![Панда и петушок Лука]() 12:12
12:12
![Полли Покет Сезон 1]() 21:30
21:30
![Хвостатые песенки]() 7:00
7:00
![Чуч-Мяуч]() 7:04
7:04
![Приключения Тайо]() 12:50
12:50
![Агент 203]() 21:08
21:08
![Оранжевая корова]() 6:30
6:30
![МиниФорс]() 0:00
0:00
![Сборники «Ну, погоди!»]() 1:10:01
1:10:01
![Зебра в клеточку]() 6:30
6:30
![Паровозик Титипо]() 13:42
13:42
![Сборники «Простоквашино»]() 1:05:35
1:05:35

 30:37
30:37Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 |
 2:41
2:41
2025-11-17 14:22
 2:52
2:52
2025-11-18 11:48
 3:17
3:17
2025-11-15 12:47
 2:37
2:37
2025-11-13 11:00
 5:23
5:23
2025-11-21 13:15
 2:44
2:44
2025-11-20 21:37
 2:30
2:30
2025-11-21 13:20
 3:30
3:30
2025-11-13 11:12
 2:06
2:06
2025-11-11 18:00
 3:13
3:13
2025-11-14 11:41
 3:49
3:49
2025-11-15 12:54
 4:01
4:01
2025-11-21 13:05
 2:34
2:34
2025-11-21 13:26
 2:11
2:11
2025-11-15 12:28
 2:47
2:47
2025-11-11 17:49
 3:32
3:32
2025-11-17 14:20
 3:28
3:28
2025-11-20 13:54
 2:47
2:47
2025-11-19 11:44
 3:32
3:32
2025-11-18 12:49
 3:14
3:14
2025-11-12 12:52
0/0
 1:32:16
1:32:16
2025-09-23 22:53
 1:31:39
1:31:39
2025-10-02 20:46
 1:40:18
1:40:18
2025-09-23 22:53
 2:09:55
2:09:55
2025-10-05 00:32
 1:22:33
1:22:33
2025-11-21 14:16
 1:34:55
1:34:55
2025-09-23 22:53
 1:33:34
1:33:34
2025-10-08 12:27
 1:39:41
1:39:41
2025-10-29 16:30
 1:34:35
1:34:35
2025-11-19 10:39
 1:28:32
1:28:32
2025-10-07 09:27
 2:15:54
2:15:54
2025-10-13 19:02
 1:39:10
1:39:10
2025-09-23 22:53
 1:49:20
1:49:20
2025-10-21 22:50
 1:18:55
1:18:55
2025-11-21 14:16
 1:46:40
1:46:40
2025-10-07 09:27
 1:53:55
1:53:55
2025-11-05 19:47
 1:45:29
1:45:29
2025-10-23 18:26
 1:23:01
1:23:01
2025-11-05 19:47
 1:56:34
1:56:34
2025-09-23 22:53
 1:44:15
1:44:15
2025-11-07 20:19
0/0
2021-09-24 16:00
 12:24
12:24
2024-11-27 13:24
 1:05:15
1:05:15
2025-09-30 13:45
 3:15
3:15
2025-06-10 13:56
2021-09-22 21:43
 11:22
11:22
2023-05-11 14:51
2021-09-22 20:39
2021-09-23 00:15
 12:12
12:12
2024-11-29 14:21
2021-09-22 23:09
 7:00
7:00
2025-06-01 11:15
 7:04
7:04
2022-03-29 15:20
 12:50
12:50
2024-12-17 13:25
 21:08
21:08
2025-01-09 16:39
 6:30
6:30
2022-03-31 18:49
 0:00
0:00
2025-11-24 23:26
 1:10:01
1:10:01
2025-07-25 20:16
 6:30
6:30
2022-03-31 13:09
 13:42
13:42
2024-11-28 14:12
 1:05:35
1:05:35
2025-10-31 17:03
0/0

