
 9:51
9:51
2025-10-25 09:00
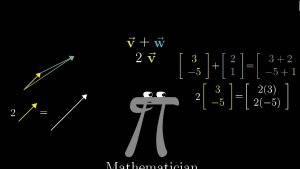
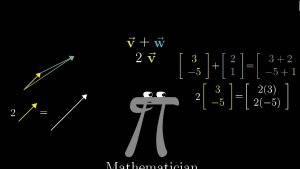 9:37
9:37
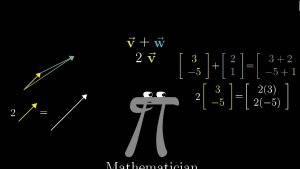
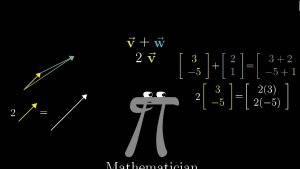 9:37
9:37
2025-10-17 09:01

 9:50
9:50

 9:50
9:50
2025-10-22 09:00

 1:27:46
1:27:46

 1:27:46
1:27:46
2020-04-22 13:21

 1:36:21
1:36:21

 1:36:21
1:36:21
2024-07-04 20:50

 3:21:60
3:21:60

 3:21:60
3:21:60
2026-01-11 22:40

 11:59:14
11:59:14

 11:59:14
11:59:14
2025-12-11 08:06

 10:54:47
10:54:47

 10:54:47
10:54:47
2025-12-26 07:13

 2:13:04
2:13:04

 2:13:04
2:13:04
2026-01-13 15:24

 1:57:17
1:57:17

 1:57:17
1:57:17
2025-12-20 21:00

 2:33:30
2:33:30

 2:33:30
2:33:30
2023-09-10 20:33

 1:38:18
1:38:18

 1:38:18
1:38:18
2025-12-30 18:00

 2:58:11
2:58:11

 2:58:11
2:58:11
2023-09-20 15:09

 1:08:43
1:08:43

 1:08:43
1:08:43
2026-01-12 11:21

 3:55:20
3:55:20

 3:55:20
3:55:20
2023-11-30 23:17

 4:02:06
4:02:06

 4:02:06
4:02:06
2025-01-04 02:00

 2:14:21
2:14:21

 2:14:21
2:14:21
2025-12-21 23:50

 3:12:39
3:12:39
![Арина Войт - Смелая (Премьера клипа 2026)]() 2:52
2:52
![Tural Everest & Руслан добрый - Верный друг (Премьера клипа 2025)]() 3:05
3:05
![Евгений Путилов - Леди ночь (Премьера клипа 2025)]() 3:33
3:33
![Turkan Abbasova - Сожженые мосты (Премьера клипа 2025)]() 3:33
3:33
![DJ Serzh - Она играла лишь со мной (Премьера клипа 2026)]() 4:12
4:12
![Murat Gamidov - Ночь подруга (Премьера клипа 2025)]() 3:04
3:04
![Алла Рид, Алексей Петрухин - А в вагоне-ресторане (Премьера клипа 2025)]() 5:14
5:14
![Шохрух Искандаров - Севдим айт (Премьера клипа 2025)]() 3:04
3:04
![DJ Serzh - Мелочи (Премьера клипа 2026)]() 3:22
3:22
![Бехруз Нурбобоев - Армон (Премьера клипа 2025)]() 7:03
7:03
![GELIK - OMG (Премьера клипа 2025)]() 2:22
2:22
![Sasha Komovich - Расскажи, Снегурочка (Премьера клипа 2025)]() 2:13
2:13
![LILI MORTO - YA YA YE (Official Video 2025)]() 2:59
2:59
![Vanilla Bun - Рядом с тобой (Премьера клипа 2025)]() 2:36
2:36
![Гунеша - Юр кетамиз (Премьера клипа 2026)]() 3:13
3:13
![Соня Белькевич, ATLANA - Поверь (Премьера 2025)]() 3:59
3:59
![Сангин - Салам (Премьера клипа 2025)]() 3:31
3:31
![Дана Лахова - Камин (Премьера клипа 2025)]() 2:09
2:09
![Merab Amzoevi - Плавно (Премьера 2025)]() 2:49
2:49
![Бахтавар - Женушка-Аленушка (Премьера клипа 2025)]() 2:39
2:39
![Астронавт | The Astronaut (2025)]() 1:30:31
1:30:31
![Баллада о маленьком игроке | Ballad of a Small Player (2025)]() 1:42:60
1:42:60
![Гарри Поттер и Тайная комната | Harry Potter and the Chamber of Secrets (2002)]() 2:54:28
2:54:28
![Всемирный потоп | Daehongsu (2025)]() 1:48:57
1:48:57
![Бугония | Bugonia (2025)]() 1:59:12
1:59:12
![Джей Келли | Jay Kelly (2025)]() 2:13:54
2:13:54
![Paзpушитeль миpoв | Worldbreaker (2025)]() 1:34:45
1:34:45
![Гарри Поттер и философский камень | Harry Potter and the Sorcerer's Stone (2001)]() 2:32:26
2:32:26
![Бегущий человек | The Running Man (2025)]() 2:16:29
2:16:29
![Сожалею о тебе | Regretting You (2025)]() 1:55:53
1:55:53
![Достать ножи: Воскрешение покойника | Wake Up Dead Man (2025)]() 2:26:20
2:26:20
![Голубая луна | Blue Moon (2025)]() 1:40:33
1:40:33
![Ловчий смерти | Deathstalker (2025)]() 1:42:60
1:42:60
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Отпуск на двоих | People We Meet on Vacation (2026)]() 1:57:55
1:57:55
![Злая. Часть 2 | Wicked: For Good (2025)]() 2:17:37
2:17:37
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Гарри Поттер и Кубок огня | Harry Potter and the Goblet of Fire (2005)]() 2:37:09
2:37:09
![Один дома 2: Затерянный в Нью-Йорке | Home Alone 2: Lost in New York (1992)]() 2:00:06
2:00:06
![Папа Супергерой Сезон 1]() 4:28
4:28
![Мотофайтеры]() 13:10
13:10
![Полли Покет Сезон 1]() 21:30
21:30
![Последний книжный магазин]() 11:20
11:20
![Школьный автобус Гордон]() 12:34
12:34
![Роботы-пожарные]() 12:31
12:31
![Хвостатые песенки]() 7:00
7:00
![Зомби Дамб]() 5:14
5:14
![Сборники «Зебра в клеточку»]() 45:30
45:30
![Умка]() 7:12
7:12
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24
![Забавные медвежата]() 13:00
13:00
![Сборники «Простоквашино»]() 1:05:30
1:05:30
![Сборники «Оранжевая корова»]() 1:05:01
1:05:01
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Оранжевая корова]() 6:30
6:30
![Команда Дино Сезон 1]() 12:08
12:08
![Пиратская школа]() 11:06
11:06
![Панда и Антилопа]() 12:08
12:08
![Агент 203]() 21:08
21:08

 3:12:39
3:12:39Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 424x240 | ||
| 640x360 | ||
| 848x480 | ||
| 1280x720 | ||
| 1920x1080 |
 2:52
2:52
2026-01-08 12:25
 3:05
3:05
2025-12-24 11:14
 3:33
3:33
2025-12-26 14:14
 3:33
3:33
2025-12-25 13:28
 4:12
4:12
2026-01-12 10:16
 3:04
3:04
2025-12-24 11:46
 5:14
5:14
2025-12-23 15:51
 3:04
3:04
2025-12-25 13:31
 3:22
3:22
2026-01-05 10:03
 7:03
7:03
2025-12-28 13:17
 2:22
2:22
2025-12-23 16:03
 2:13
2:13
2026-01-01 11:00
 2:59
2:59
2025-12-24 11:18
 2:36
2:36
2025-12-23 16:09
 3:13
3:13
2026-01-12 10:24
 3:59
3:59
2025-12-28 13:25
 3:31
3:31
2025-12-23 15:57
 2:09
2:09
2025-12-23 14:17
 2:49
2:49
2025-12-24 11:24
 2:39
2:39
2025-12-28 13:29
0/0
 1:30:31
1:30:31
2026-01-14 15:48
 1:42:60
1:42:60
2025-10-31 10:53
 2:54:28
2:54:28
2025-12-25 15:41
 1:48:57
1:48:57
2026-01-14 15:48
 1:59:12
1:59:12
2025-11-29 02:45
 2:13:54
2:13:54
2025-12-08 13:26
 1:34:45
1:34:45
2025-11-27 19:40
 2:32:26
2:32:26
2025-12-25 15:41
 2:16:29
2:16:29
2025-12-17 23:52
 1:55:53
1:55:53
2025-12-17 23:52
 2:26:20
2:26:20
2025-12-20 21:33
 1:40:33
1:40:33
2025-12-17 23:52
 1:42:60
1:42:60
2025-12-03 17:17
 1:47:36
1:47:36
2025-12-25 17:49
 1:57:55
1:57:55
2026-01-14 15:48
 2:17:37
2:17:37
2026-01-14 15:48
 1:47:25
1:47:25
2025-11-27 03:58
 1:18:55
1:18:55
2025-11-21 14:16
 2:37:09
2:37:09
2025-12-25 15:40
 2:00:06
2:00:06
2025-12-25 15:39
0/0
2021-09-22 21:52
 13:10
13:10
2024-11-27 14:57
2021-09-22 23:09
 11:20
11:20
2025-09-12 10:05
 12:34
12:34
2024-12-02 14:42
2021-09-23 00:12
 7:00
7:00
2025-06-01 11:15
 5:14
5:14
2024-11-28 13:12
 45:30
45:30
2025-12-11 18:53
 7:12
7:12
2026-01-12 17:15
 12:24
12:24
2024-11-27 13:24
 13:00
13:00
2024-12-02 13:15
 1:05:30
1:05:30
2025-06-27 13:20
 1:05:01
1:05:01
2025-12-12 12:24
 13:00
13:00
2024-11-28 16:19
 6:30
6:30
2025-12-30 19:54
2021-09-22 22:29
 11:06
11:06
2022-04-01 15:56
 12:08
12:08
2025-06-10 14:59
 21:08
21:08
2025-01-09 16:39
0/0

