
 4:02
4:02
2024-06-23 03:45

 3:20
3:20

 3:20
3:20
2024-06-23 04:03

 5:22
5:22

 5:22
5:22
2024-06-23 04:09

 1:12:18
1:12:18

 1:12:18
1:12:18
2023-11-21 19:32
![ТЕСТ НА ПСИХИКУ НЕ БЛЕВАНИ CHALLENGE]() 7:27
7:27
 7:27
7:27
2016-08-26 14:53

 13:45
13:45

 13:45
13:45
2024-04-06 00:17

 23:40
23:40

 23:40
23:40
2023-12-25 09:23
![Мультфильмы для детей My - Cartoons For Kids Tom and Jerry - Episode 55]() 4:07
4:07
 4:07
4:07
2018-08-30 16:27

 11:12
11:12

 11:12
11:12
2023-11-10 17:29
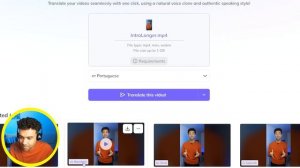
 2:11
2:11

 2:11
2:11
2023-12-30 05:48

 3:21:60
3:21:60

 3:21:60
3:21:60
2026-01-11 22:40

 2:58:11
2:58:11

 2:58:11
2:58:11
2023-09-20 15:09

 1:47:32
1:47:32

 1:47:32
1:47:32
2025-12-24 09:18

 11:16:29
11:16:29

 11:16:29
11:16:29
2025-05-23 08:04

 5:36
5:36

 5:36
5:36
2026-01-15 01:44

 3:12:39
3:12:39

 3:12:39
3:12:39
2023-09-15 21:20

 2:32:19
2:32:19

 2:32:19
2:32:19
2023-09-10 18:25

 3:48:10
3:48:10
![SOPRANO Турецкого & Кай Син - Ах мамочка, на саночках (Премьера клипа 2026)]() 3:40
3:40
![Евгений Григорьев ЖЕКА, Алёна Егорова - Синхронит любовь (Премьера клипа 2026)]() 3:24
3:24
![DJ Serzh - Мелочи (Премьера клипа 2026)]() 3:22
3:22
![Рада Рай - Мечта (Премьера клипа 2025)]() 4:43
4:43
![Рустам Батербиев - Стерва-ночь (Премьера клипа 2026)]() 2:24
2:24
![Эльчин Кулиев - Сладкие сказки (Премьера клипа 2026)]() 4:08
4:08
![Дурдона Курбонова - Дил (Премьера клипа 2025)]() 3:33
3:33
![Андрей Храмов - Я приглашу тебя на танец (Премьера клипа 2026)]() 4:01
4:01
![DJ Serzh - Котолюция (Премьера клипа 2026)]() 3:30
3:30
![AY YOLA, ALSOU - Ay, bylbylym (Премьера клипа 2026)]() 4:08
4:08
![Низомчон Азимов - Меравам (Премьера клипа 2026)]() 2:42
2:42
![Сарвар Мадримов - Бора-бора (Премьера клипа 2026)]() 3:09
3:09
![Арина Войт - Смелая (Премьера клипа 2026)]() 2:52
2:52
![Виктория Качур - Жду тебя (Премьера клипа 2025)]() 3:40
3:40
![Надежда Мельянцева - Судьбы ирония (Премьера 2025)]() 3:02
3:02
![Бахтавар - Женушка-Аленушка (Премьера клипа 2025)]() 2:39
2:39
![ARTIX - Последний снег (Премьера клипа 2026)]() 3:17
3:17
![Как на Новый год в селе девочки гуляли]() 4:58
4:58
![Соня Белькевич, ATLANA - Поверь (Премьера 2025)]() 3:59
3:59
![DJ Serzh - Она играла лишь со мной (Премьера клипа 2026)]() 4:12
4:12
![Кристи | Christy (2025)]() 2:15:04
2:15:04
![Гарри Поттер и Кубок огня | Harry Potter and the Goblet of Fire (2005)]() 2:37:09
2:37:09
![Шматрица | Matrix (1999) (Гоблин)]() 2:17:10
2:17:10
![Достать ножи: Воскрешение покойника | Wake Up Dead Man (2025)]() 2:26:20
2:26:20
![Семейный план 2 | The Family Plan 2 (2025)]() 1:46:14
1:46:14
![Игры Биста. 2 сезон, 5 серия | Beast Games 2 season]() 49:20
49:20
![Пять ночей с Фредди 2 | Five Nights at Freddy's 2 (2025)]() 1:44:11
1:44:11
![Бегущий человек | The Running Man (2025)]() 2:16:29
2:16:29
![Игры Биста. 2 сезон, 3 серия | Beast Games 2 season]() 57:01
57:01
![Один дома | Home Alone (1990)]() 1:43:02
1:43:02
![Гарри Поттер и Дары Смерти: Часть I | Harry Potter and the Deathly Hallows - Part 1 (2010)]() 2:26:10
2:26:10
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Злая. Часть 2 | Wicked: For Good (2025)]() 2:17:37
2:17:37
![Голубая луна | Blue Moon (2025)]() 1:40:33
1:40:33
![Ловчий смерти | Deathstalker (2025)]() 1:42:60
1:42:60
![Боже. Как. Смешно. | Oh. What. Fun. (2025)]() 1:47:58
1:47:58
![Один дома 2: Затерянный в Нью-Йорке | Home Alone 2: Lost in New York (1992)]() 2:00:06
2:00:06
![Бугония | Bugonia (2025)]() 1:59:12
1:59:12
![Вдохновитель | The Mastermind (2025)]() 1:50:21
1:50:21
![Лакомый кусок | The Rip (2026)]() 1:52:50
1:52:50
![Рэй и пожарный патруль Сезон 1]() 13:27
13:27
![Сборники «Приключения Пети и Волка»]() 1:17:53
1:17:53
![Агент 203]() 21:08
21:08
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Хвостатые песенки]() 7:00
7:00
![Пингвиненок Пороро]() 7:42
7:42
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24
![Супер Зак]() 11:38
11:38
![Крутиксы]() 11:00
11:00
![Забавные медвежата]() 13:00
13:00
![Неодети]() 11:27
11:27
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![МиниФорс Сезон 1]() 13:12
13:12
![Пип и Альба Сезон 1]() 11:02
11:02
![Роботы-пожарные]() 12:31
12:31
![Зебра в клеточку]() 6:30
6:30
![Минифорс. Сила динозавров]() 12:51
12:51
![Сборники «Оранжевая корова»]() 1:05:01
1:05:01
![Панда и петушок Лука]() 12:12
12:12
![Мартышкины]() 7:10
7:10

 3:48:10
3:48:10Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 426x240 | ||
| 640x360 | ||
| 854x480 |
 3:40
3:40
2026-01-20 10:50
 3:24
3:24
2026-01-15 12:53
 3:22
3:22
2026-01-05 10:03
 4:43
4:43
2025-12-30 11:35
 2:24
2:24
2026-01-15 13:21
 4:08
4:08
2026-01-15 10:48
 3:33
3:33
2025-12-27 10:17
 4:01
4:01
2026-01-15 13:30
 3:30
3:30
2026-01-20 10:30
 4:08
4:08
2026-01-07 22:29
 2:42
2:42
2026-01-04 11:59
 3:09
3:09
2026-01-14 15:26
 2:52
2:52
2026-01-08 12:25
 3:40
3:40
2025-12-30 11:27
 3:02
3:02
2025-12-26 14:02
 2:39
2:39
2025-12-28 13:29
 3:17
3:17
2026-01-20 10:41
 4:58
4:58
2026-01-01 11:35
 3:59
3:59
2025-12-28 13:25
 4:12
4:12
2026-01-12 10:16
0/0
 2:15:04
2:15:04
2025-12-12 14:01
 2:37:09
2:37:09
2025-12-25 15:40
 2:17:10
2:17:10
2025-11-17 12:53
 2:26:20
2:26:20
2025-12-20 21:33
 1:46:14
1:46:14
2025-11-26 06:44
 49:20
49:20
2026-01-23 13:36
 1:44:11
1:44:11
2025-12-25 22:29
 2:16:29
2:16:29
2025-12-17 23:52
 57:01
57:01
2026-01-07 23:55
 1:43:02
1:43:02
2025-12-25 15:40
 2:26:10
2:26:10
2025-12-25 15:40
 2:32:29
2:32:29
2025-11-17 11:22
 2:17:37
2:17:37
2026-01-14 15:48
 1:40:33
1:40:33
2025-12-17 23:52
 1:42:60
1:42:60
2025-12-03 17:17
 1:47:58
1:47:58
2025-12-09 13:32
 2:00:06
2:00:06
2025-12-25 15:39
 1:59:12
1:59:12
2025-11-29 02:45
 1:50:21
1:50:21
2025-12-17 00:55
 1:52:50
1:52:50
2026-01-23 09:26
0/0
2021-09-22 23:51
 1:17:53
1:17:53
2025-12-19 23:55
 21:08
21:08
2025-01-09 16:39
2021-09-22 20:39
 7:00
7:00
2025-06-01 11:15
 7:42
7:42
2024-12-17 12:21
 12:24
12:24
2024-11-27 13:24
2021-09-22 22:07
 11:00
11:00
2022-07-25 18:59
 13:00
13:00
2024-12-02 13:15
 11:27
11:27
2025-10-10 18:25
2021-09-22 21:03
2021-09-23 00:15
2021-09-22 23:37
2021-09-23 00:12
 6:30
6:30
2022-03-31 13:09
 12:51
12:51
2024-11-27 16:39
 1:05:01
1:05:01
2025-12-12 12:24
 12:12
12:12
2024-11-29 14:21
 7:10
7:10
2025-12-30 18:33
0/0

