 9:25
9:25
2022-03-05 12:20
![Расстояние от точки до плоскости]() 7:02
7:02
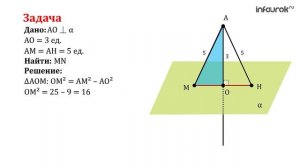 7:02
7:02
2021-03-19 17:50

 9:09
9:09

 9:09
9:09
2020-10-25 18:10

 2:00:06
2:00:06

 2:00:06
2:00:06
2026-01-26 21:00

 10:25:31
10:25:31

 10:25:31
10:25:31
2025-05-02 07:58

 11:56:60
11:56:60

 11:56:60
11:56:60
2025-08-29 07:40

 11:59:14
11:59:14

 11:59:14
11:59:14
2025-12-11 08:06

 5:36
5:36

 5:36
5:36
2026-01-15 01:44

 2:40:56
2:40:56

 2:40:56
2:40:56
2023-09-10 18:55

 9:22:58
9:22:58

 9:22:58
9:22:58
2025-12-23 08:07

 3:50:16
3:50:16

 3:50:16
3:50:16
2024-08-19 15:47

 2:37:05
2:37:05

 2:37:05
2:37:05
2023-09-10 20:03

 11:51:08
11:51:08

 11:51:08
11:51:08
2025-12-05 07:23

 4:23:18
4:23:18

 4:23:18
4:23:18
2024-02-16 17:06

 5:37:49
5:37:49

 5:37:49
5:37:49
2013-01-18 02:37

 1:14:36
1:14:36

 1:14:36
1:14:36
2026-01-26 11:58

 4:02:06
4:02:06

 4:02:06
4:02:06
2025-01-04 02:00

 48:53
48:53
![DJ Serzh - Котолюция (Премьера клипа 2026)]() 3:30
3:30
![БАХТАВАР - В белом платье (Премьера клипа 2026)]() 3:17
3:17
![ARTIX - Последний снег (Премьера клипа 2026)]() 3:17
3:17
![Гунеша - Юр кетамиз (Премьера клипа 2026)]() 3:13
3:13
![Самира Сариева - Хоп-хоп (Премьера клипа 2026)]() 3:20
3:20
![Дана Лахова - Ай, яй, яй (Премьера клипа 2026)]() 2:53
2:53
![Алишер Файз - Биё-биё (Премьера клипа 2026)]() 3:16
3:16
![Азамат Пхешхов, Руслан Шанов - Родная (Премьера клипа 2026)]() 3:25
3:25
![Misty - Замело (Премьера клипа 2026)]() 2:44
2:44
![Наталья Влади, Любовь Рыбкина - В жизни успеть (Премьера клипа 2026)]() 2:37
2:37
![Ramon, Вагаршак Асриян - Кавказский бит (Премьера клипа 2026)]() 2:03
2:03
![Syuzi Dzhaginian - Сегодня я плачу (Премьера клипа 2026)]() 2:57
2:57
![Антон и Альфия - Январская вьюга (Премьера клипа 2026)]() 3:32
3:32
![Григорий Герасимов - Я другой (Премьера клипа 2026)]() 3:32
3:32
![Эльчин Кулиев - Сладкие сказки (Премьера клипа 2026)]() 4:08
4:08
![KhaliF - Сияй (Премьера клипа 2026)]() 2:22
2:22
![Zhamil Turan - Одна на миллион (Премьера клипа 2026)]() 2:57
2:57
![Медина Мелик - Дура (Премьера клипа 2026)]() 2:41
2:41
![Андрей Храмов - Я приглашу тебя на танец (Премьера клипа 2026)]() 4:01
4:01
![Вусал Мирзаев - Ты моя (Премьера клипа 2026)]() 2:14
2:14
![Всемирный потоп | Daehongsu (2025)]() 1:48:57
1:48:57
![Безжалостная | Stone Cold Fox (2025)]() 1:25:31
1:25:31
![Франкенштейн | Frankenstein (2025)]() 2:32:29
2:32:29
![Побег из плена | Prisoner of War (2025)]() 1:52:58
1:52:58
![Бугония | Bugonia (2025)]() 1:59:12
1:59:12
![Прощай Джун | Goodbye June (2025)]() 1:56:04
1:56:04
![Достать ножи: Воскрешение покойника | Wake Up Dead Man (2025)]() 2:26:20
2:26:20
![Хищник: Планета смерти | Predator: Badlands (2025)]() 1:47:25
1:47:25
![Бегущий человек | The Running Man (2025)]() 2:16:29
2:16:29
![Доверие | Trust (2025)]() 1:30:44
1:30:44
![Пять ночей с Фредди 2 | Five Nights at Freddy's 2 (2025)]() 1:44:11
1:44:11
![Сожалею о тебе | Regretting You (2025)]() 1:55:53
1:55:53
![Кристи | Christy (2025)]() 2:15:04
2:15:04
![Гарри Поттер и Принц-полукровка | Harry Potter and the Half-Blood Prince (2009)]() 2:33:36
2:33:36
![Один дома 2: Затерянный в Нью-Йорке | Home Alone 2: Lost in New York (1992)]() 2:00:06
2:00:06
![Супергеройское кино | Superhero Movie (2008)]() 1:22:33
1:22:33
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Голубая луна | Blue Moon (2025)]() 1:40:33
1:40:33
![Гарри Поттер и Тайная комната | Harry Potter and the Chamber of Secrets (2002)]() 2:54:28
2:54:28
![Вдохновитель | The Mastermind (2025)]() 1:50:21
1:50:21
![Сборники «Приключения Пети и Волка»]() 1:17:53
1:17:53
![Новогодние мультики – Союзмультфильм]() 7:04
7:04
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Сборники «Оранжевая корова»]() 1:05:01
1:05:01
![Енотки]() 7:08
7:08
![Лудлвилль]() 7:05
7:05
![Люк - путешественник во времени]() 1:19:50
1:19:50
![Зебра в клеточку]() 6:30
6:30
![МиниФорс]() 0:00
0:00
![Команда Дино. Исследователи Сезон 1]() 13:10
13:10
![Мотофайтеры]() 13:10
13:10
![Простоквашино. Финансовая грамотность]() 3:27
3:27
![Папа Супергерой Сезон 1]() 4:28
4:28
![Забавные медвежата]() 13:00
13:00
![Сборники «Умка»]() 3:09:60
3:09:60
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Умка]() 7:11
7:11
![Мартышкины]() 7:10
7:10
![Панда и Антилопа]() 12:08
12:08
![Монсики]() 6:30
6:30

 48:53
48:53Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 426x240 | ||
| 640x360 |
 3:30
3:30
2026-01-20 10:30
 3:17
3:17
2026-01-28 09:57
 3:17
3:17
2026-01-20 10:41
 3:13
3:13
2026-01-12 10:24
 3:20
3:20
2026-01-28 10:04
 2:53
2:53
2026-01-22 11:17
 3:16
3:16
2026-01-28 11:55
 3:25
3:25
2026-01-23 19:30
 2:44
2:44
2026-01-28 12:02
 2:37
2:37
2026-01-22 10:58
 2:03
2:03
2026-01-20 10:47
 2:57
2:57
2026-01-28 11:50
 3:32
3:32
2026-01-28 09:47
 3:32
3:32
2026-01-14 15:22
 4:08
4:08
2026-01-15 10:48
 2:22
2:22
2026-01-22 11:38
 2:57
2:57
2026-01-14 15:11
 2:41
2:41
2026-01-13 10:54
 4:01
4:01
2026-01-15 13:30
 2:14
2:14
2026-01-15 12:40
0/0
 1:48:57
1:48:57
2026-01-14 15:48
 1:25:31
1:25:31
2025-11-10 21:11
 2:32:29
2:32:29
2025-11-17 11:22
 1:52:58
1:52:58
2026-01-26 14:34
 1:59:12
1:59:12
2025-11-29 02:45
 1:56:04
1:56:04
2026-01-21 16:22
 2:26:20
2:26:20
2025-12-20 21:33
 1:47:25
1:47:25
2025-11-27 03:58
 2:16:29
2:16:29
2025-12-17 23:52
 1:30:44
1:30:44
2025-12-17 23:52
 1:44:11
1:44:11
2025-12-25 22:29
 1:55:53
1:55:53
2025-12-17 23:52
 2:15:04
2:15:04
2025-12-12 14:01
 2:33:36
2:33:36
2025-12-25 15:40
 2:00:06
2:00:06
2025-12-25 15:39
 1:22:33
1:22:33
2025-11-21 14:16
 1:46:45
1:46:45
2026-01-19 12:39
 1:40:33
1:40:33
2025-12-17 23:52
 2:54:28
2:54:28
2025-12-25 15:41
 1:50:21
1:50:21
2025-12-17 00:55
0/0
 1:17:53
1:17:53
2025-12-19 23:55
 7:04
7:04
2023-07-25 00:09
 4:33
4:33
2024-12-17 16:56
 1:05:01
1:05:01
2025-12-12 12:24
 7:08
7:08
2025-12-30 21:34
 7:05
7:05
2025-12-30 20:49
 1:19:50
1:19:50
2024-12-17 16:00
 6:30
6:30
2022-03-31 13:09
 0:00
0:00
2026-01-29 06:59
2021-09-22 22:45
 13:10
13:10
2024-11-27 14:57
 3:27
3:27
2024-12-07 11:00
2021-09-22 21:52
 13:00
13:00
2024-12-02 13:15
 3:09:60
3:09:60
2025-12-11 18:53
2021-09-22 20:39
 7:11
7:11
2026-01-20 10:00
 7:10
7:10
2025-12-30 18:33
 12:08
12:08
2025-06-10 14:59
 6:30
6:30
2022-03-29 19:16
0/0

