
 13:42
13:42
2023-12-02 08:48
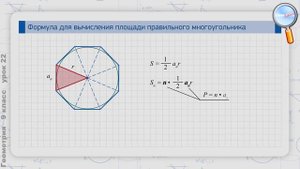
 5:02
5:02

 5:02
5:02
2023-09-08 17:18

 4:02
4:02

 4:02
4:02
2025-02-17 16:30

 2:00:06
2:00:06

 2:00:06
2:00:06
2026-01-26 21:00

 3:12:39
3:12:39

 3:12:39
3:12:39
2023-12-21 11:54

 10:25:31
10:25:31

 10:25:31
10:25:31
2025-05-02 07:58

 1:47:32
1:47:32

 1:47:32
1:47:32
2025-12-24 09:18

 5:36
5:36

 5:36
5:36
2026-01-15 01:44

 2:32:19
2:32:19

 2:32:19
2:32:19
2023-09-10 18:25

 2:58:11
2:58:11

 2:58:11
2:58:11
2023-09-20 15:09

 3:48:10
3:48:10

 3:48:10
3:48:10
2023-09-18 01:16

 1:35:38
1:35:38

 1:35:38
1:35:38
2026-01-30 10:57

 11:59:14
11:59:14

 11:59:14
11:59:14
2025-12-11 08:06

 3:10:29
3:10:29

 3:10:29
3:10:29
2025-12-20 10:48

 2:01:48
2:01:48

 2:01:48
2:01:48
2023-12-14 11:09

 2:21:44
2:21:44

 2:21:44
2:21:44
2023-09-10 19:20

 3:55:20
3:55:20

 3:55:20
3:55:20
2023-11-30 23:17

 1:48:45
1:48:45
![Самир Санаев - Дилрабо (Премьера клипа 2026)]() 4:17
4:17
![KhaliF - Сияй (Премьера клипа 2026)]() 2:22
2:22
![Zhamil Turan - Одна на миллион (Премьера клипа 2026)]() 2:57
2:57
![ANIVAR - Маски (Премьера клипа 2026)]() 2:13
2:13
![Самира Сариева - Хоп-хоп (Премьера клипа 2026)]() 3:20
3:20
![Сарвар Мадримов - Бора-бора (Премьера клипа 2026)]() 3:09
3:09
![Tural Everest, Руслан Добрый - Не хочу (Премьера клипа 2026)]() 2:46
2:46
![Андрей Храмов - Я приглашу тебя на танец (Премьера клипа 2026)]() 4:01
4:01
![Tural Everest - Забыла (Премьера клипа 2026)]() 2:44
2:44
![Оксана Ковалевская - Ты меня не ищи (Премьера клипа 2026)]() 3:05
3:05
![Артур Халатов - Красивая любовь (Премьера клипа 2026)]() 3:23
3:23
![Артур Бесаев - Там где горы (Премьера клипа 2026)]() 2:15
2:15
![NAIMAN - Тебя украду (Премьера клипа 2026)]() 2:28
2:28
![DJ Serzh - Она играла лишь со мной (Премьера клипа 2026)]() 4:12
4:12
![Ирина Круг и Вика Ветер - Крестик (Премьера клипа 2026)]() 3:53
3:53
![Jazzdauren - Юность (Премьера клипа 2026)]() 2:44
2:44
![Вусал Мирзаев - Ты моя (Премьера клипа 2026)]() 2:14
2:14
![Дана Лахова - Ай, яй, яй (Премьера клипа 2026)]() 2:53
2:53
![Арина Войт - Смелая (Премьера клипа 2026)]() 2:52
2:52
![Кравц - 99 проблем (Премьера клипа 2026)]() 2:30
2:30
![Сожалею о тебе | Regretting You (2025)]() 1:55:53
1:55:53
![Прощай Джун | Goodbye June (2025)]() 1:56:04
1:56:04
![Голубая луна | Blue Moon (2025)]() 1:40:33
1:40:33
![Достать ножи: Воскрешение покойника | Wake Up Dead Man (2025)]() 2:26:20
2:26:20
![Мелодия их мечты | Song Sung Blue (2025)]() 2:12:15
2:12:15
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Гарри Поттер и узник Азкабана | Harry Potter and the Prisoner of Azkaban (2004)]() 2:21:46
2:21:46
![Кровь на границе | Frontier Crucible (2025)]() 2:04:36
2:04:36
![Отпуск на двоих | People We Meet on Vacation (2026)]() 1:57:55
1:57:55
![Вдохновитель | The Mastermind (2025)]() 1:50:21
1:50:21
![Гарри Поттер и Кубок огня | Harry Potter and the Goblet of Fire (2005)]() 2:37:09
2:37:09
![Зверополис 2 | Zootopia 2 (2025)]() 1:47:36
1:47:36
![Ловчий смерти | Deathstalker (2025)]() 1:42:60
1:42:60
![Гарри Поттер и философский камень | Harry Potter and the Sorcerer's Stone (2001)]() 2:32:26
2:32:26
![Побег из плена | Prisoner of War (2025)]() 1:52:58
1:52:58
![Сират | Sirât (2025)]() 1:54:52
1:54:52
![Злая. Часть 2 | Wicked: For Good (2025)]() 2:17:37
2:17:37
![Носферату | Nosferatu (2024)]() 2:12:40
2:12:40
![Бугония | Bugonia (2025)]() 1:59:12
1:59:12
![Тихое место: День первый | A Quiet Place: Day One (2024)]() 1:39:30
1:39:30
![Мультфильмы военных лет | Специальный проект к 80-летию Победы]() 7:20
7:20
![Сборники «Простоквашино»]() 1:05:30
1:05:30
![Енотки]() 7:08
7:08
![Пип и Альба Сезон 1]() 11:02
11:02
![Пакман в мире привидений]() 21:37
21:37
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Чуч-Мяуч]() 7:04
7:04
![Роботы-пожарные]() 12:31
12:31
![Тёплая анимация | Новая авторская анимация Союзмультфильма]() 10:46
10:46
![Агент 203]() 21:08
21:08
![МиниФорс]() 0:00
0:00
![Новогодние мультики – Союзмультфильм]() 7:04
7:04
![Команда Дино Сезон 2]() 12:31
12:31
![Лудлвилль]() 7:05
7:05
![Кадеты Баданаму Сезон 1]() 11:50
11:50
![Врумиз. 1 сезон]() 13:10
13:10
![Зомби Дамб]() 5:14
5:14
![Панда и петушок Лука]() 12:12
12:12
![Корги по имени Моко. Новый питомец]() 3:28
3:28
![Пластилинки]() 25:31
25:31

 1:48:45
1:48:45Скачать Видео с Рутуба / RuTube
| 426x240 | ||
| 640x360 | ||
| 854x480 | ||
| 1280x720 | ||
| 1920x1080 |
 4:17
4:17
2026-01-28 12:17
 2:22
2:22
2026-01-22 11:38
 2:57
2:57
2026-01-14 15:11
 2:13
2:13
2026-01-10 14:36
 3:20
3:20
2026-01-28 10:04
 3:09
3:09
2026-01-14 15:26
 2:46
2:46
2026-01-28 12:09
 4:01
4:01
2026-01-15 13:30
 2:44
2:44
2026-01-23 18:15
 3:05
3:05
2026-01-24 13:42
 3:23
3:23
2026-01-23 17:57
 2:15
2:15
2026-01-16 16:50
 2:28
2:28
2026-01-28 12:37
 4:12
4:12
2026-01-12 10:16
 3:53
3:53
2026-01-23 18:04
 2:44
2:44
2026-01-28 11:45
 2:14
2:14
2026-01-15 12:40
 2:53
2:53
2026-01-22 11:17
 2:52
2:52
2026-01-08 12:25
 2:30
2:30
2026-01-14 15:04
0/0
 1:55:53
1:55:53
2025-12-17 23:52
 1:56:04
1:56:04
2026-01-21 16:22
 1:40:33
1:40:33
2025-12-17 23:52
 2:26:20
2:26:20
2025-12-20 21:33
 2:12:15
2:12:15
2026-01-21 16:23
 1:46:45
1:46:45
2026-01-19 12:39
 2:21:46
2:21:46
2025-12-25 15:40
 2:04:36
2:04:36
2026-01-26 14:34
 1:57:55
1:57:55
2026-01-14 15:48
 1:50:21
1:50:21
2025-12-17 00:55
 2:37:09
2:37:09
2025-12-25 15:40
 1:47:36
1:47:36
2025-12-25 17:49
 1:42:60
1:42:60
2025-12-03 17:17
 2:32:26
2:32:26
2025-12-25 15:41
 1:52:58
1:52:58
2026-01-26 14:34
 1:54:52
1:54:52
2026-01-26 14:35
 2:17:37
2:17:37
2026-01-14 15:48
 2:12:40
2:12:40
2026-01-23 18:44
 1:59:12
1:59:12
2025-11-29 02:45
 1:39:30
1:39:30
2026-01-23 18:43
0/0
 7:20
7:20
2025-05-03 12:34
 1:05:30
1:05:30
2025-06-27 13:20
 7:08
7:08
2025-12-30 21:34
2021-09-22 23:37
 21:37
21:37
2024-11-28 17:35
 13:00
13:00
2024-11-28 16:19
 7:04
7:04
2022-03-29 15:20
2021-09-23 00:12
 10:46
10:46
2022-06-07 11:02
 21:08
21:08
2025-01-09 16:39
 0:00
0:00
2026-01-31 17:08
 7:04
7:04
2023-07-25 00:09
2021-09-22 22:40
 7:05
7:05
2025-12-30 20:49
2021-09-22 21:17
2021-09-24 16:00
 5:14
5:14
2024-11-28 13:12
 12:12
12:12
2024-11-29 14:21
 3:28
3:28
2025-01-09 17:01
 25:31
25:31
2022-04-01 14:30
0/0

