
 27:58
27:58
2025-09-20 10:00

 8:30
8:30

 8:30
8:30
2025-09-12 15:00

 1:55:45
1:55:45

 1:55:45
1:55:45
2025-09-16 20:14

 24:23
24:23

 24:23
24:23
2025-09-11 09:20

 3:20
3:20

 3:20
3:20
2025-09-11 10:37

 34:56
34:56

 34:56
34:56
2025-09-12 16:44

 5:52
5:52

 5:52
5:52
2025-09-25 23:50

 0:36
0:36

 0:36
0:36
2025-09-26 18:00

 27:32
27:32

 27:32
27:32
2025-09-22 15:05

 19:12
19:12

 19:12
19:12
2025-09-11 14:41

 4:18
4:18

 4:18
4:18
2025-09-21 11:49
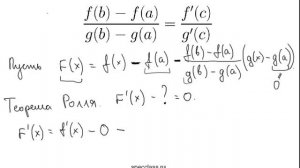
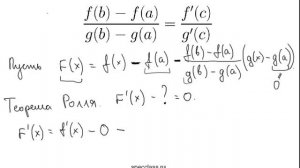 5:59
5:59
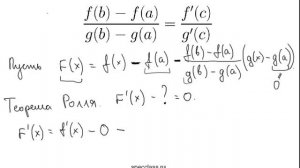
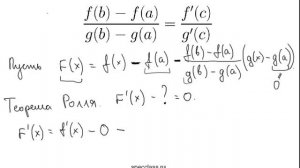 5:59
5:59
2023-09-21 12:03

 1:57:38
1:57:38

 1:57:38
1:57:38
2025-09-15 15:22
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14
![Самые жестокие завоеватели в истории? / [История по Чёрному]](https://pic.rutubelist.ru/video/2025-09-22/8f/5b/8f5b92672e89625eec19c110dbe923b0.jpg?width=300)
 55:14
55:14
2025-09-23 12:00

 1:50:16
1:50:16

 1:50:16
1:50:16
2025-09-15 14:19

 5:30
5:30

 5:30
5:30
2025-09-24 07:00

 27:57
27:57

 27:57
27:57
2025-09-16 16:21

 2:15
2:15
![Зафар Эргашов - Мусофирда каридим (Премьера клипа 2025)]() 4:58
4:58
![Анна Бершадская - Новая я (Премьера клипа 2025)]() 2:41
2:41
![Anette - Erjanik em (Official Video 2025)]() 3:36
3:36
![МАРАТ & АРНИ - Стала женой (Премьера клипа 2025)]() 3:51
3:51
![Владимир Ждамиров - Чифирок (Премьера клипа 2025)]() 3:49
3:49
![Игорь Кибирев - Пьяная ночь (Премьера клипа 2025)]() 3:08
3:08
![TASSO - Таю (Премьера клипа 2025)]() 3:23
3:23
![Мария Зайцева - Жаль моя (Премьера клипа 2025)]() 4:25
4:25
![Жалолиддин Ахмадалиев - Тонг отгунча (Премьера клипа 2025)]() 4:44
4:44
![Женя Белоусова - Кто тебе сказал (Премьера клипа 2025)]() 3:27
3:27
![Артур Пирожков - ALARM (Премьера клипа 2025)]() 3:22
3:22
![MIA BOYKA - А он такой (Премьера клипа 2025)]() 2:24
2:24
![Фаррух Хамраев - Отажоним булсайди (Премьера клипа 2025)]() 3:08
3:08
![Zhamil Turan - Капали (Премьера клипа 2025)]() 3:08
3:08
![Премьера клипа! Артур Пирожков - ALARM]() 3:22
3:22
![M1DNITE - Ghost Touch]() 3:36
3:36
![Ганишер Раззоков - Дилижон (Премьера клипа 2025)]() 3:46
3:46
![Taylor Swift - The Fate of Ophelia (Official Video 2025)]() 3:58
3:58
![Премьера клипа! Мария Зайцева – Жаль моя]() 4:25
4:25
![Ольга Бузова - Не надо (Премьера клипа 2025)]() 3:15
3:15
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Город демонов | Oni Goroshi (2025)]() 1:48:12
1:48:12
![Французский любовник | French Lover (2025)]() 2:02:20
2:02:20
![Мир юрского периода Возрождение | Jurassic World: Rebirth (2025)]() 2:13:53
2:13:53
![Богомол | Samagwi (2025)]() 1:53:29
1:53:29
![Диспетчер | Relay (2025)]() 1:51:56
1:51:56
![Дьявол | Diablo (2025)]() 1:31:20
1:31:20
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Обитель | The Home (2025)]() 1:34:43
1:34:43
![Финикийская схема | The Phoenician Scheme (2025)]() 1:41:27
1:41:27
![Синг-Синг | Sing Sing (2024)]() 1:46:50
1:46:50
![Плохие парни 2 | The Bad Guys 2 (2025)]() 1:43:51
1:43:51
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Источник вечной молодости | Fountain of Youth (2025)]() 2:05:22
2:05:22
![Заклятие 4: Последний обряд | The Conjuring: Last Rites (2025)]() 2:15:54
2:15:54
![Бабули | Nonnas (2025)]() 1:54:10
1:54:10
![Опустошение | Havoc (2025)]() 1:47:26
1:47:26
![F1 (2025)]() 2:35:53
2:35:53
![M3GAN 2 | M3GAN 2.0 (2025)]() 2:00:03
2:00:03
![Счастливчик Гилмор 2 | Happy Gilmore (2025)]() 1:57:36
1:57:36
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Папа Супергерой Сезон 1]() 4:28
4:28
![Игрушечный полицейский Сезон 1]() 7:19
7:19
![Забавные медвежата]() 13:00
13:00
![Пиратская школа]() 11:06
11:06
![Агент 203]() 21:08
21:08
![Команда Дино Сезон 1]() 12:08
12:08
![Поймай Тинипин! Королевство эмоций]() 12:24
12:24
![Панда и петушок Лука]() 12:12
12:12
![Школьный автобус Гордон]() 12:34
12:34
![Сандра - сказочный детектив Сезон 1]() 13:52
13:52
![Пип и Альба. Приключения в Соленой Бухте! Сезон 1]() 11:02
11:02
![Отважные мишки]() 13:00
13:00
![Пип и Альба Сезон 1]() 11:02
11:02
![Лудлвилль]() 7:09
7:09
![Артур и дети круглого стола]() 11:22
11:22
![Приключения Пети и Волка]() 11:00
11:00
![Сборники «Умка»]() 1:20:52
1:20:52
![Сборники «Простоквашино»]() 1:04:60
1:04:60
![Панда и Антилопа]() 12:08
12:08

 2:15
2:15Скачать видео
| 426x206 | ||
| 640x310 | ||
| 854x414 |
 4:58
4:58
2025-10-18 10:31
 2:41
2:41
2025-10-22 14:02
 3:36
3:36
2025-10-18 10:11
 3:51
3:51
2025-10-16 11:41
 3:49
3:49
2025-10-16 10:37
 3:08
3:08
2025-10-16 11:32
 3:23
3:23
2025-10-16 10:00
 4:25
4:25
2025-10-17 11:28
 4:44
4:44
2025-10-19 10:46
 3:27
3:27
2025-10-16 11:15
 3:22
3:22
2025-10-20 14:44
 2:24
2:24
2025-10-14 12:10
 3:08
3:08
2025-10-18 10:28
 3:08
3:08
2025-10-22 14:26
 3:22
3:22
2025-10-20 15:41
 3:36
3:36
2025-10-12 18:00
 3:46
3:46
2025-10-14 11:30
 3:58
3:58
2025-10-17 11:48
 4:25
4:25
2025-10-18 17:45
 3:15
3:15
2025-10-18 10:02
0/0
 1:35:11
1:35:11
2025-10-13 12:06
 1:48:12
1:48:12
2025-08-12 17:48
 2:02:20
2:02:20
2025-10-01 12:06
 2:13:53
2:13:53
2025-08-09 11:00
 1:53:29
1:53:29
2025-10-01 12:06
 1:51:56
1:51:56
2025-09-24 11:35
 1:31:20
1:31:20
2025-06-25 14:54
 1:54:40
1:54:40
2025-09-24 11:35
 1:34:43
1:34:43
2025-09-09 12:49
 1:41:27
1:41:27
2025-06-30 07:40
 1:46:50
1:46:50
2025-02-11 12:05
 1:43:51
1:43:51
2025-08-26 16:18
 2:09:55
2:09:55
2025-10-05 00:32
 2:05:22
2:05:22
2025-05-30 00:57
 2:15:54
2:15:54
2025-10-13 19:02
 1:54:10
1:54:10
2025-06-20 15:43
 1:47:26
1:47:26
2025-08-02 13:33
 2:35:53
2:35:53
2025-08-26 11:45
 2:00:03
2:00:03
2025-07-19 19:23
 1:57:36
1:57:36
2025-08-21 17:43
0/0
 4:33
4:33
2024-12-17 16:56
2021-09-22 21:52
2021-09-22 21:03
 13:00
13:00
2024-12-02 13:15
 11:06
11:06
2022-04-01 15:56
 21:08
21:08
2025-01-09 16:39
2021-09-22 22:29
 12:24
12:24
2024-11-27 13:24
 12:12
12:12
2024-11-29 14:21
 12:34
12:34
2024-12-02 14:42
2021-09-22 20:39
2021-09-22 23:36
 13:00
13:00
2024-11-29 13:39
2021-09-22 23:37
 7:09
7:09
2023-07-06 19:20
 11:22
11:22
2023-05-11 14:51
 11:00
11:00
2022-04-01 17:59
 1:20:52
1:20:52
2025-09-19 17:54
 1:04:60
1:04:60
2025-09-02 13:47
 12:08
12:08
2025-06-10 14:59
0/0

