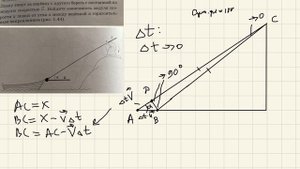
 9:44
9:44
2024-01-29 06:22

 2:10
2:10

 2:10
2:10
2023-12-22 21:47

 13:38
13:38

 13:38
13:38
2024-04-24 04:33

 3:45
3:45

 3:45
3:45
2024-12-16 21:26
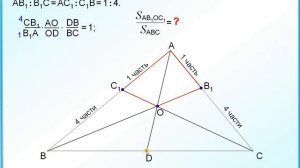
 15:48
15:48

 15:48
15:48
2023-12-28 13:15

 3:23
3:23

 3:23
3:23
2024-12-01 11:30
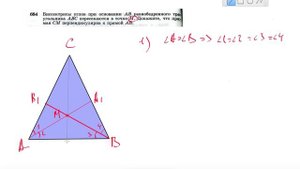
 1:56
1:56

 1:56
1:56
2023-12-22 02:21

 5:26
5:26

 5:26
5:26
2025-02-05 17:15

 0:11
0:11

 0:11
0:11
2024-02-02 02:24

 4:00
4:00

 4:00
4:00
2024-05-21 07:00

 3:48
3:48

 3:48
3:48
2023-10-17 04:21
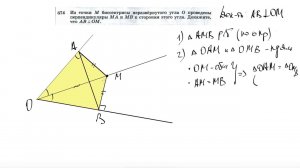
 3:17
3:17

 3:17
3:17
2020-04-24 11:15
 7:06
7:06

 7:06
7:06
2023-09-13 20:55

 9:21
9:21

 9:21
9:21
2023-08-30 20:40

 6:02
6:02

 6:02
6:02
2014-06-19 15:31
 5:24
5:24

 5:24
5:24
2023-09-20 21:21

 2:21
2:21

 2:21
2:21
2023-07-04 23:04

 30:45
30:45
![Lx24 - Сберегу (Премьера клипа 2025)]() 2:57
2:57
![Enrasta, Мурат Тхагалегов - Калым (Премьера клипа 2025)]() 3:07
3:07
![Анвар Нишонов - Тулкилар (Премьера клипа 2025)]() 3:38
3:38
![INSTASAMKA - KISS MY DISS (Премьера клипа 2025)]() 3:14
3:14
![Эльдар Долаев - Ранила (Премьера клипа 2025)]() 3:02
3:02
![Ирина Аллегрова, Игорь Крутой — У окна]() 2:53
2:53
![W24 - I Gotta Feeling]() 3:49
3:49
![mzlff — мало-помалу]() 3:57
3:57
![Сардор Хайруллаев - Келма (Премьера клипа 2025)]() 4:10
4:10
![ХАБИБ - Шаганэ (Премьера клипа 2025)]() 2:49
2:49
![МИРОСЛАВА, ЗЛАТА и НАСТЯ КОШ - ЦАРЕВНА ЗАБАВА]() 2:11
2:11
![UMARO, Сангин - Брат мой (Премьера клипа 2025)]() 3:16
3:16
![TAEYONG - 501 Special Video]() 2:50
2:50
![Азамат Ражабов - Отам (Премьера клипа 2025)]() 4:38
4:38
![Xeko - Увы, чужая (Премьера клипа 2025)]() 2:10
2:10
![Премьера клипа! Моя Мишель - Иногда]() 3:12
3:12
![Антон и Альфия - Сентиментальный мотив (Премьера клипа 2025)]() 3:35
3:35
![Премьера клипа! ХАБИБ - Шаганэ]() 2:49
2:49
![M1DNITE - Ghost Touch]() 3:36
3:36
![Сергей Одинцов - Любимая, родная (Премьера клипа 2025)]() 3:32
3:32
![Порочный круг (2025)]() 1:43:41
1:43:41
![Последний клиент]() 1:33:23
1:33:23
![Алиса в Стране чудес: Все части 1, 2 (фильмы)]() 4:14:09
4:14:09
![Монстры: История Эда Гейна (2025) (мини-сериал)]() 7:26:60
7:26:60
![Скандальный взлом (2019)]() 1:54:14
1:54:14
![Школьный автобус (2025)]() 2:09:51
2:09:51
![Пойман с поличным (2025)]() 1:46:41
1:46:41
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Аббатство Даунтон 3 (2025)]() 2:03:57
2:03:57
![Гонка (2013) 1080]() 1:37:04
1:37:04
![Финикийская схема (2025)]() 1:41:00
1:41:00
![Битва проклятых (2013)]() 1:28:46
1:28:46
![Облако (2024)]() 2:04:02
2:04:02
![Отец]() 1:32:56
1:32:56
![Скелеты Железного острова]() 1:25:19
1:25:19
![Комната (2003)]() 1:39:52
1:39:52
![Волынь (2016)]() 2:28:56
2:28:56
![Посредники]() 2:04:01
2:04:01
![Как бы беременна (2025) Netflix]() 1:40:02
1:40:02
![Вивариум (2019)]() 1:38:34
1:38:34
![Иллюзионист (2010) / L'illusionniste]()
 1:19:53
1:19:53
![Альфа и Омега 4: Легенда о Зубастой Пещере (2014) / Alpha and Omega 4]()
 45:14
45:14
![Девочки из Эквестрии. Пропуск за кулисы для Сансет (2018) / Equestria Girls. Sunset's Backstage Pass]()
 44:08
44:08
![Земля до начала времён 5: Таинственный остров (1997) / The Land Before Time V]()
 1:13:30
1:13:30
![Волшебный парк Джун (2019) / Wonder Park]()
 1:25:17
1:25:17
![Барби: Виртуальный мир (2017) / Barbie Video Game Hero]()
 1:12:19
1:12:19
![Земля до начала времён 8: Великая стужа (2001) / The Land Before Time VIII]()
 1:15:49
1:15:49
![Земля до начала времён 9: Путешествие к Большой Воде (2002) / The Land Before Time IX]()
 1:14:38
1:14:38
![Ночная жуть Тайни Тун (1995) / Tiny Toon Night Ghoulery]()
 43:38
43:38
![Земля до начала времён 12: Великий День птиц (2006) / The Land Before Time XII]()
 1:20:30
1:20:30
![Земля до начала времён 4: Путешествие в Землю Туманов (1996) / The Land Before Time IV]()
 1:13:52
1:13:52
![Науэль и волшебная книга (2020) / Nauel and the Magic Book]()
 1:37:06
1:37:06
![Девочки из Эквестрии. Легенды вечнозелёного леса (2016) / Equestria Girls. Legend of Everfree]()
 1:13:14
1:13:14
![Земля до начала времён 3: В поисках воды (1995) / The Land Before Time III]()
 1:10:48
1:10:48
![Земля до начала времён 7: Камень Холодного Огня (2000) / The Land Before Time VII]()
 1:14:10
1:14:10
![Эти прекрасные мультяшки: Рождественский выпуск (1992) / It's a Wonderful Christmas Special]()
 22:22
22:22
![Шерлок Гномс (2018) / Sherlock Gnomes]()
 1:26:19
1:26:19
![Гномео и Джульетта (2011) / Gnomeo & Juliet]()
 1:23:51
1:23:51
![Смурфики (2011) / The Smurfs]()
 1:42:44
1:42:44
![Земля до начала времён 10: Великая миграция (2003) / The Land Before Time X]()
 1:24:21
1:24:21

 30:45
30:45Скачать видео
| 256x144 | ||
| 426x240 | ||
| 640x360 | ||
| 854x480 | ||
| 1280x720 | ||
| 1920x1080 |
 2:57
2:57
2025-10-11 12:26
 3:07
3:07
2025-10-11 12:03
 3:38
3:38
2025-10-11 12:45
 3:14
3:14
2025-10-10 12:28
 3:02
3:02
2025-10-10 12:56
2025-10-05 18:36
2025-10-12 18:28
2025-10-05 18:36
 4:10
4:10
2025-10-13 12:31
 2:49
2:49
2025-10-10 12:36
2025-10-05 18:35
 3:16
3:16
2025-10-10 13:04
2025-10-08 16:00
 4:38
4:38
2025-10-11 12:52
 2:10
2:10
2025-10-10 12:50
2025-10-08 20:01
 3:35
3:35
2025-10-09 09:15
 2:49
2:49
2025-10-10 09:59
2025-10-12 18:00
 3:32
3:32
2025-10-07 11:46
0/0
 1:43:41
1:43:41
2025-10-13 12:39
 1:33:23
1:33:23
2025-10-13 11:36
 4:14:09
4:14:09
2025-10-06 16:06
 7:26:60
7:26:60
2025-10-05 20:29
 1:54:14
1:54:14
2025-10-01 18:56
 2:09:51
2:09:51
2025-10-04 10:38
 1:46:41
1:46:41
2025-10-04 09:54
 1:35:11
1:35:11
2025-10-13 12:06
 2:03:57
2:03:57
2025-10-05 21:44
2025-10-05 17:38
 1:41:00
1:41:00
2025-10-05 21:22
2025-10-03 22:51
 2:04:02
2:04:02
2025-10-12 13:06
 1:32:56
1:32:56
2025-10-13 11:37
 1:25:19
1:25:19
2025-10-13 11:18
 1:39:52
1:39:52
2025-10-08 18:11
 2:28:56
2:28:56
2025-10-08 21:04
 2:04:01
2:04:01
2025-10-13 11:37
 1:40:02
1:40:02
2025-10-08 19:42
 1:38:34
1:38:34
2025-10-01 13:01
0/0

 1:19:53
1:19:53
2025-10-11 18:00

 45:14
45:14
2025-10-12 18:00

 44:08
44:08
Девочки из Эквестрии. Пропуск за кулисы для Сансет (2018) / Equestria Girls. Sunset's Backstage Pass
2025-10-03 18:00

 1:13:30
1:13:30
2025-09-20 18:00

 1:25:17
1:25:17
2025-09-08 18:00

 1:12:19
1:12:19
2025-09-05 18:00

 1:15:49
1:15:49
2025-09-26 18:00

 1:14:38
1:14:38
2025-09-28 18:00

 43:38
43:38
2025-09-09 18:00

 1:20:30
1:20:30
2025-10-04 18:00

 1:13:52
1:13:52
2025-09-17 18:00

 1:37:06
1:37:06
2025-10-05 18:00

 1:13:14
1:13:14
2025-10-01 18:00

 1:10:48
1:10:48
2025-09-15 18:00

 1:14:10
1:14:10
2025-09-24 18:00

 22:22
22:22
2025-09-11 18:00

 1:26:19
1:26:19
2025-09-25 18:00

 1:23:51
1:23:51
2025-09-10 18:00

 1:42:44
1:42:44
2025-09-27 18:00

 1:24:21
1:24:21
2025-09-30 18:00
0/0

