
 14:21
14:21
2024-09-12 13:48

 4:51
4:51

 4:51
4:51
2024-11-07 09:30

 25:42
25:42

 25:42
25:42
2025-09-12 17:00

 10:38
10:38

 10:38
10:38
2024-09-12 12:55

 50:03
50:03

 50:03
50:03
2025-12-10 10:01

 23:38
23:38

 23:38
23:38
2022-10-21 19:48
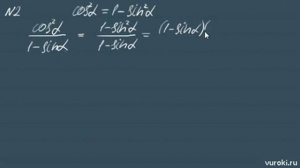
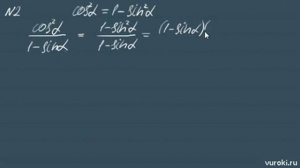 7:27
7:27
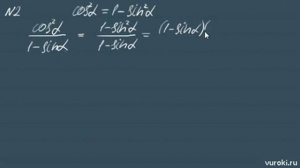
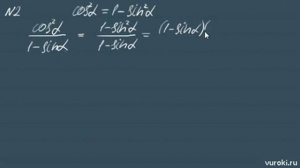 7:27
7:27
2023-09-12 20:33
 1:25
1:25

 1:25
1:25
2023-09-07 13:25

 3:30
3:30

 3:30
3:30
2023-09-27 23:46

 6:51
6:51

 6:51
6:51
2025-05-20 17:34

 13:32
13:32

 13:32
13:32
2025-09-23 18:30

 24:34
24:34

 24:34
24:34
2025-09-22 17:30

 23:44
23:44

 23:44
23:44
2022-10-20 21:06

 1:41:35
1:41:35

 1:41:35
1:41:35
2025-02-11 18:05

 26:38
26:38

 26:38
26:38
2023-02-10 06:12

 7:22
7:22

 7:22
7:22
2023-09-26 16:49

 11:34
11:34

 11:34
11:34
2018-01-24 13:02

 2:04
2:04
![Женя Белоусова - Мы больше не рядом (Премьера клипа 2025)]() 2:50
2:50
![BITTUEV - Песни по радио (Премьера клипа 2025)]() 3:05
3:05
![MILEN - Я соскучился (Премьера 2025)]() 4:04
4:04
![Акрамжон Хотамов - Ёдат мекунам (Премьера клипа 2025)]() 3:22
3:22
![Артур Бесаев - Все пройдет (Премьера клипа 2025)]() 3:44
3:44
![Макс Вертиго, PAKALENA - Разбиться о скалы (Премьера клипа 2025)]() 3:18
3:18
![Tural Everest - Любить не хочет (Премьера клипа 2025)]() 2:55
2:55
![NLO, Leonid Rudenko - Зеленоглазое такси (Премьера клипа 2025)]() 2:22
2:22
![Оксана Джелиева - Курортный роман (Премьера клипа 2025)]() 2:45
2:45
![Вусал Мирзаев - Я с тобой (Премьера клипа 2025)]() 2:30
2:30
![Ислам Итляшев - Пантера (Премьера клипа 2025)]() 3:07
3:07
![Zhamil Turan - Ты не моя (Премьера клипа 2025)]() 2:37
2:37
![BEST guruhi - Yana kim bor (Official Video 2025)]() 3:22
3:22
![Зардияна - Севган бахтли буларму (Премьера клипа 2025)]() 3:28
3:28
![Асия - Дом (Премьера клипа 2025)]() 6:45
6:45
![Отабек Холматов - Хамманинг уз дарди бор (Премьера клипа 2025)]() 3:10
3:10
![Альберт Эркенов - Мои шрамы (Премьера клипа 2025)]() 3:15
3:15
![Ruslan Bakinskiy & Vuqar Islam - Я Забыл (Премьера клипа 2025)]() 4:01
4:01
![Нодирбек Шомирзаев - Севги (Премьера клипа 2025)]() 4:32
4:32
![Инна Вальтер - Не проиграть себе (Премьера клипа 2025)]() 3:04
3:04
![Терминатор 2: Судный день | Terminator 2: Judgment Day (1991) (Гоблин)]() 2:36:13
2:36:13
![Хищник | Predator (1987) (Гоблин)]() 1:46:40
1:46:40
![Тот самый | Him (2025)]() 1:36:20
1:36:20
![Боже. Как. Смешно. | Oh. What. Fun. (2025)]() 1:47:58
1:47:58
![Очень голодные игры | The Starving Games (2013)]() 1:18:55
1:18:55
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Богомол | Samagwi (2025)]() 1:53:29
1:53:29
![Семейный план 2 | The Family Plan 2 (2025)]() 1:46:14
1:46:14
![Протокол выхода | Exit Protocol (2025)]() 1:24:45
1:24:45
![Трон: Арес | Tron: Ares (2025)]() 1:52:27
1:52:27
![Мужчина у меня в подвале | The Man in My Basement (2025)]() 1:54:48
1:54:48
![Орудия | Weapons (2025)]() 2:08:34
2:08:34
![Плохой Cанта 2 | Bad Santa 2 (2016) (Гоблин)]() 1:28:32
1:28:32
![Супергеройское кино | Superhero Movie (2008)]() 1:22:33
1:22:33
![Рука, качающая колыбель | The Hand That Rocks the Cradle (2025)]() 1:44:57
1:44:57
![Крысы: Ведьмачья история | The Rats: A Witcher Tale (2025)]() 1:23:01
1:23:01
![Все дьяволы здесь | All the Devils are Here (2025)]() 1:31:39
1:31:39
![Чумовая пятница 2 | Freakier Friday (2025)]() 1:50:38
1:50:38
![Paзpушитeль миpoв | Worldbreaker (2025)]() 1:34:45
1:34:45
![Джей Келли | Jay Kelly (2025)]() 2:13:54
2:13:54
![Панда и Антилопа]() 12:08
12:08
![Умка]() 7:11
7:11
![Пиратская школа]() 11:06
11:06
![Супер Дино]() 12:41
12:41
![МиниФорс]() 0:00
0:00
![Панда и петушок Лука]() 12:12
12:12
![Пип и Альба Сезон 1]() 11:02
11:02
![Сборники «Простоквашино»]() 1:05:35
1:05:35
![Забавные медвежата]() 13:00
13:00
![Оранжевая корова]() 6:30
6:30
![Истории Баданаму Сезон 1]() 10:02
10:02
![Школьный автобус Гордон]() 12:34
12:34
![Неодети]() 11:27
11:27
![Тайны Медовой долины]() 7:01
7:01
![Пластилинки]() 25:31
25:31
![Пингвиненок Пороро]() 7:42
7:42
![Енотки]() 7:04
7:04
![Псэмми. Пять детей и волшебство Сезон 1]() 12:17
12:17
![Хвостатые песенки]() 7:00
7:00
![Корги по имени Моко. Новый питомец]() 3:28
3:28

 2:04
2:04Скачать Видео с Рутуба / RuTube
| 256x144 | ||
| 432x232 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 2:50
2:50
2025-12-04 11:41
 3:05
3:05
2025-12-06 16:02
 4:04
4:04
2025-11-28 10:52
 3:22
3:22
2025-11-28 11:08
 3:44
3:44
2025-12-10 00:19
 3:18
3:18
2025-12-04 11:49
 2:55
2:55
2025-12-05 14:44
 2:22
2:22
2025-12-08 15:50
 2:45
2:45
2025-11-27 12:36
 2:30
2:30
2025-11-28 11:04
 3:07
3:07
2025-11-29 13:34
 2:37
2:37
2025-12-04 11:11
 3:22
3:22
2025-12-06 15:34
 3:28
3:28
2025-12-04 12:09
 6:45
6:45
2025-11-29 13:44
 3:10
3:10
2025-11-27 12:58
 3:15
3:15
2025-12-08 19:45
 4:01
4:01
2025-12-10 10:13
 4:32
4:32
2025-11-28 11:11
 3:04
3:04
2025-12-10 00:16
0/0
 2:36:13
2:36:13
2025-10-07 09:27
 1:46:40
1:46:40
2025-10-07 09:27
 1:36:20
1:36:20
2025-10-09 20:02
 1:47:58
1:47:58
2025-12-09 13:32
 1:18:55
1:18:55
2025-11-21 14:16
 2:09:55
2:09:55
2025-10-05 00:32
 1:53:29
1:53:29
2025-10-01 12:06
 1:46:14
1:46:14
2025-11-26 06:44
 1:24:45
1:24:45
2025-11-13 23:26
 1:52:27
1:52:27
2025-11-06 18:12
 1:54:48
1:54:48
2025-10-01 15:17
 2:08:34
2:08:34
2025-09-24 22:05
 1:28:32
1:28:32
2025-10-07 09:27
 1:22:33
1:22:33
2025-11-21 14:16
 1:44:57
1:44:57
2025-10-29 16:30
 1:23:01
1:23:01
2025-11-05 19:47
 1:31:39
1:31:39
2025-10-02 20:46
 1:50:38
1:50:38
2025-10-16 16:08
 1:34:45
1:34:45
2025-11-27 19:40
 2:13:54
2:13:54
2025-12-08 13:26
0/0
 12:08
12:08
2025-06-10 14:59
 7:11
7:11
2025-01-13 11:05
 11:06
11:06
2022-04-01 15:56
 12:41
12:41
2024-11-28 12:54
 0:00
0:00
2025-12-11 09:02
 12:12
12:12
2024-11-29 14:21
2021-09-22 23:37
 1:05:35
1:05:35
2025-10-31 17:03
 13:00
13:00
2024-12-02 13:15
 6:30
6:30
2022-03-31 18:49
2021-09-22 21:29
 12:34
12:34
2024-12-02 14:42
 11:27
11:27
2025-10-10 18:25
 7:01
7:01
2022-03-30 17:25
 25:31
25:31
2022-04-01 14:30
 7:42
7:42
2024-12-17 12:21
 7:04
7:04
2022-03-29 18:22
2021-09-22 22:23
 7:00
7:00
2025-06-01 11:15
 3:28
3:28
2025-01-09 17:01
0/0

