
 0:55
0:55
2024-07-07 03:05

 7:32
7:32

 7:32
7:32
2023-12-02 07:11
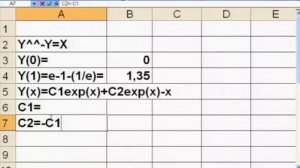
 1:06:13
1:06:13

 1:06:13
1:06:13
2023-12-02 04:19

 5:13
5:13

 5:13
5:13
2024-10-10 11:29

 3:05
3:05

 3:05
3:05
2025-02-07 05:32

 4:17
4:17

 4:17
4:17
2024-01-31 06:24

 5:48
5:48

 5:48
5:48
2024-02-01 13:00

 19:59
19:59

 19:59
19:59
2024-01-30 03:21

 22:19
22:19

 22:19
22:19
2024-01-22 09:24
 4:15
4:15

 4:15
4:15
2023-10-28 01:44

 4:49
4:49

 4:49
4:49
2024-03-14 19:35

 26:40
26:40

 26:40
26:40
2023-09-04 08:50
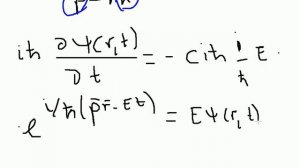
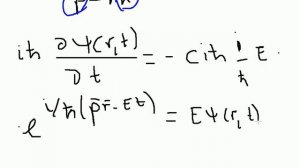 8:23
8:23
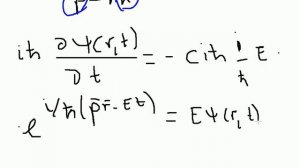
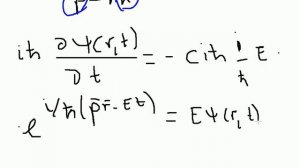 8:23
8:23
2023-09-07 13:18

 2:45
2:45

 2:45
2:45
2022-05-21 06:29
 7:30
7:30

 7:30
7:30
2023-09-04 10:37

 15:29
15:29

 15:29
15:29
2022-11-15 12:49
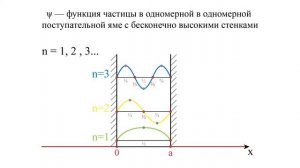
 2:18
2:18

 2:18
2:18
2022-05-20 18:51
![Промо, всего один рекламный ролик (Канал Disney, 13.12.22)[IPTVrip]](https://pic.rutubelist.ru/video/7c/4b/7c4b36a3fd56a2099d79aaf09d2fb729.jpg?width=300)
 0:35
0:35
![Жалолиддин Ахмадалиев - Тонг отгунча (Премьера клипа 2025)]() 4:44
4:44
![Анвар Нишонов - Тулкилар (Премьера клипа 2025)]() 3:38
3:38
![Анна Бершадская - Новая я (Премьера клипа 2025)]() 2:41
2:41
![Наталья Влади - А я такая (Премьера клипа 2025)]() 2:21
2:21
![INSTASAMKA - AGENT GIRL (Премьера клипа 2025)]() 3:24
3:24
![Владимир Ждамиров - Чифирок (Премьера клипа 2025)]() 3:49
3:49
![Taylor Swift - The Fate of Ophelia (Official Video 2025)]() 3:58
3:58
![Фати Царикаева - Стамбул (Премьера клипа 2025)]() 2:57
2:57
![5sta Family - Антидот (Премьера клипа 2025)]() 3:33
3:33
![Сардор Хайруллаев - Келма (Премьера клипа 2025)]() 4:10
4:10
![Фаррух Хамраев - Отажоним булсайди (Премьера клипа 2025)]() 3:08
3:08
![Игорь Кибирев - Пьяная ночь (Премьера клипа 2025)]() 3:08
3:08
![ИЮЛА - Ты был прав (Премьера клипа 2025)]() 2:21
2:21
![Zhamil Turan - Капали (Премьера клипа 2025)]() 3:08
3:08
![MARSO - Дура (Премьера клипа 2025)]() 3:05
3:05
![Олег Семенов - Бархатный сезон (Премьера клипа 2025)]() 3:51
3:51
![NAIMAN - Уникальная (Премьера клипа 2025)]() 2:37
2:37
![Сарвар Азим - Бахтим (Премьера клипа 2025)]() 4:10
4:10
![Рустам Батербиев - Пора расстаться (Премьера клипа 2025)]() 2:38
2:38
![Зара - Я несла свою беду (Премьера клипа 2025)]() 3:36
3:36
![Актер | The Actor (2025)]() 1:38:13
1:38:13
![Как приручить дракона | How to Train Your Dragon (2025)]() 2:05:23
2:05:23
![Сверху вниз | Highest 2 Lowest (2025)]() 2:13:21
2:13:21
![Бабули | Nonnas (2025)]() 1:54:10
1:54:10
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![Ночная сучка | Nightbitch (2024)]() 1:39:36
1:39:36
![Электрический штат | The Electric State (2025)]() 2:08:34
2:08:34
![Счастливчик Гилмор 2 | Happy Gilmore (2025)]() 1:57:36
1:57:36
![Вне юрисдикции | Exterritorial (2025)]() 1:49:09
1:49:09
![Тот самый | Him (2025)]() 1:36:20
1:36:20
![Путь рыцаря | A Knight's War (2025)]() 1:43:53
1:43:53
![Стив | Steve (2025)]() 1:33:34
1:33:34
![Полный нокаут | K.O. (2025)]() 1:26:53
1:26:53
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Девушка из каюты №10 | The Woman in Cabin 10 (2025)]() 1:35:11
1:35:11
![Милая вилла | La Dolce Villa (2025)]() 1:39:20
1:39:20
![Синг-Синг | Sing Sing (2024)]() 1:46:50
1:46:50
![M3GAN 2 | M3GAN 2.0 (2025)]() 2:00:03
2:00:03
![Кирпич | Brick]() 1:40:58
1:40:58
![Углубление (2025)]() 2:07:52
2:07:52
![Панда и Антилопа]() 12:08
12:08
![МиниФорс Сезон 1]() 13:12
13:12
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Роботы-пожарные]() 12:31
12:31
![Оранжевая корова]() 6:30
6:30
![Артур и дети круглого стола]() 11:22
11:22
![Енотки]() 7:04
7:04
![Крутиксы]() 11:00
11:00
![Школьный автобус Гордон]() 12:34
12:34
![Сборники «Зебра в клеточку»]() 45:30
45:30
![Пакман в мире привидений]() 21:37
21:37
![Лудлвилль]() 7:09
7:09
![Пластилинки]() 25:31
25:31
![Минифорс. Сила динозавров]() 12:51
12:51
![Забавные медвежата]() 13:00
13:00
![Простоквашино]() 6:48
6:48
![Пиратская школа]() 11:06
11:06
![Паровозик Титипо]() 13:42
13:42
![Команда Дино. Исследователи Сезон 2]() 13:26
13:26
![Синдбад и семь галактик Сезон 1]() 10:23
10:23
![Промо, всего один рекламный ролик (Канал Disney, 13.12.22)[IPTVrip]](https://pic.rutubelist.ru/video/7c/4b/7c4b36a3fd56a2099d79aaf09d2fb729.jpg?width=300)
 0:35
0:35Скачать видео
| 320x240 | ||
| 480x360 | ||
| 640x480 | ||
| 960x720 | ||
| 1440x1080 |
 4:44
4:44
2025-10-19 10:46
 3:38
3:38
2025-10-11 12:45
 2:41
2:41
2025-10-22 14:02
 2:21
2:21
2025-10-14 11:07
 3:24
3:24
2025-10-17 11:33
 3:49
3:49
2025-10-16 10:37
 3:58
3:58
2025-10-17 11:48
 2:57
2:57
2025-10-15 10:54
 3:33
3:33
2025-10-22 13:57
 4:10
4:10
2025-10-13 12:31
 3:08
3:08
2025-10-18 10:28
 3:08
3:08
2025-10-16 11:32
 2:21
2:21
2025-10-18 10:16
 3:08
3:08
2025-10-22 14:26
 3:05
3:05
2025-10-17 11:37
 3:51
3:51
2025-10-16 10:57
 2:37
2:37
2025-10-14 10:48
 4:10
4:10
2025-10-11 12:49
 2:38
2:38
2025-10-16 11:06
 3:36
3:36
2025-10-18 10:07
0/0
 1:38:13
1:38:13
2025-04-09 20:04
 2:05:23
2:05:23
2025-07-18 18:28
 2:13:21
2:13:21
2025-09-09 12:49
 1:54:10
1:54:10
2025-06-20 15:43
 1:29:27
1:29:27
2025-09-07 22:44
 1:39:36
1:39:36
2025-01-01 23:55
 2:08:34
2:08:34
2025-03-21 19:58
 1:57:36
1:57:36
2025-08-21 17:43
 1:49:09
1:49:09
2025-08-13 10:53
 1:36:20
1:36:20
2025-10-09 20:02
 1:43:53
1:43:53
2025-07-16 20:59
 1:33:34
1:33:34
2025-10-08 12:27
 1:26:53
1:26:53
2025-06-20 15:43
 1:54:40
1:54:40
2025-09-24 11:35
 1:35:11
1:35:11
2025-10-13 12:06
 1:39:20
1:39:20
2025-03-21 12:00
 1:46:50
1:46:50
2025-02-11 12:05
 2:00:03
2:00:03
2025-07-19 19:23
 1:40:58
1:40:58
2025-08-03 10:48
 2:07:52
2:07:52
2025-02-18 18:05
0/0
 12:08
12:08
2025-06-10 14:59
2021-09-23 00:15
 13:00
13:00
2024-11-28 16:19
2021-09-23 00:12
 6:30
6:30
2022-03-31 18:49
 11:22
11:22
2023-05-11 14:51
 7:04
7:04
2022-03-29 18:22
 11:00
11:00
2022-07-25 18:59
 12:34
12:34
2024-12-02 14:42
 45:30
45:30
2025-09-17 18:49
 21:37
21:37
2024-11-28 17:35
 7:09
7:09
2023-07-06 19:20
 25:31
25:31
2022-04-01 14:30
 12:51
12:51
2024-11-27 16:39
 13:00
13:00
2024-12-02 13:15
 6:48
6:48
2025-10-17 10:00
 11:06
11:06
2022-04-01 15:56
 13:42
13:42
2024-11-28 14:12
2021-09-22 22:54
2021-09-22 23:09
0/0

