
 4:57
4:57
2024-11-01 16:30

 8:51
8:51

 8:51
8:51
2022-12-06 13:31

 20:40
20:40

 20:40
20:40
2025-01-13 19:11

 7:37
7:37

 7:37
7:37
2023-09-27 01:11
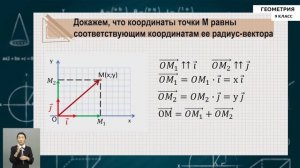
 23:57
23:57

 23:57
23:57
2023-09-11 18:23

 2:30
2:30

 2:30
2:30
2024-04-25 20:58
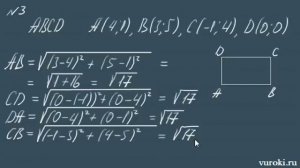
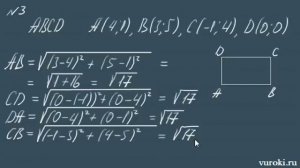 4:42
4:42
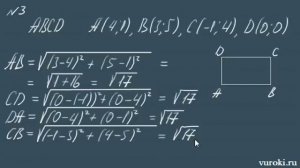
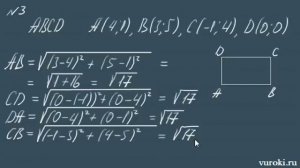 4:42
4:42
2023-09-28 18:32

 8:53
8:53

 8:53
8:53
2023-09-27 17:39

 2:04
2:04

 2:04
2:04
2025-05-08 20:07
 9:51
9:51

 9:51
9:51
2023-09-23 16:49

 5:15
5:15

 5:15
5:15
2024-11-01 18:00
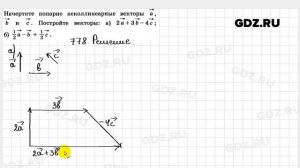
 4:17
4:17

 4:17
4:17
2023-12-28 14:47

 11:13
11:13

 11:13
11:13
2024-10-15 18:20

 7:30
7:30

 7:30
7:30
2023-12-01 10:19

 6:40
6:40

 6:40
6:40
2023-12-01 10:19

 5:40
5:40

 5:40
5:40
2023-12-01 10:19

 4:22
4:22

 4:22
4:22
2025-02-03 16:15

 1:45
1:45
![Жасурбек Мирзажонов - Суймаганга суйкалдим (Премьера клипа 2025)]() 5:45
5:45
![Нодир Иброҳимов - Жоним мени (Премьера клипа 2025)]() 4:01
4:01
![Искандар Шокалонов - Дустларим (Премьера 2025)]() 4:00
4:00
![Илёс Юнусий - Каранг она якинларим (Премьера клипа 2025)]() 3:36
3:36
![Мужик из СИБИРИ (Александр Конев) - Не прощу (Премьера клипа 2025)]() 2:39
2:39
![Анжелика Агурбаш - Утро (Премьера клипа 2025)]() 3:33
3:33
![Хабибулло Хамроз - Хуп деб куёринг (Премьера клипа 2025)]() 4:04
4:04
![Рустам Нахушев, Зульфия Чотчаева - Каюсь (Премьера клипа 2025)]() 3:20
3:20
![NIKA DUBIK, Winter Spirit - Искры (Премьера клипа 2025)]() 4:27
4:27
![A'Studio – Она не виновата (Премьера клипа 2025)]() 2:13
2:13
![Бьянка - Бренд (Премьера клипа 2025)]() 2:29
2:29
![Bruno Mars ft. Ed Sheeran – Home to You (Official Video 2025)]() 3:25
3:25
![Зара - Танго о двух влюбленных кораблях (Премьера клипа 2025)]() 3:10
3:10
![Артур Халатов - Девочка моя (Премьера клипа 2025)]() 2:37
2:37
![ARTIX - Ай, джана-джана (Премьера клипа 2025)]() 2:24
2:24
![Гор Мартиросян - 101 роза (Премьера клипа 2025)]() 4:26
4:26
![Равшанбек Балтаев - Кастюм (Премьера клипа 2025)]() 3:59
3:59
![Сергей Одинцов - Девочка любимая (Премьера клипа 2025)]() 3:56
3:56
![Cvetocek7 - Запретила (Премьера клипа 2025)]() 2:49
2:49
![BITTUEV - Не плачь (Премьера клипа 2025)]() 2:18
2:18
![Голос любви | Aline (2020)]() 2:05:43
2:05:43
![Псы войны | Hounds of War (2024)]() 1:34:38
1:34:38
![Пойман с поличным | Caught Stealing (2025)]() 1:46:45
1:46:45
![Фантастическая четвёрка: Первые шаги | The Fantastic Four: First Steps (2025)]() 1:54:40
1:54:40
![Свинья | Pig (2021)]() 1:31:23
1:31:23
![Чумовая пятница 2 | Freakier Friday (2025)]() 1:50:38
1:50:38
![Школьный автобус | The Lost Bus (2025)]() 2:09:55
2:09:55
![Мальчишник в Таиланде | Changeland (2019)]() 1:25:47
1:25:47
![Храброе сердце | Braveheart (1995)]() 2:57:46
2:57:46
![Только ты | All of You (2025)]() 1:38:22
1:38:22
![Когда ты закончишь спасать мир | When You Finish Saving the World (2022)]() 1:27:40
1:27:40
![Никто 2 | Nobody 2 (2025)]() 1:29:27
1:29:27
![Голый пистолет | The Naked Gun (2025)]() 1:26:24
1:26:24
![Терминатор 2: Судный день | Terminator 2: Judgment Day (1991) (Гоблин)]() 2:36:13
2:36:13
![Рука, качающая колыбель | The Hand That Rocks the Cradle (2025)]() 1:44:57
1:44:57
![Баллада о маленьком игроке | Ballad of a Small Player (2025)]() 1:42:60
1:42:60
![Хищник | Predator (1987) (Гоблин)]() 1:46:40
1:46:40
![Свинтусы | The Twits (2025)]() 1:42:50
1:42:50
![Кей-поп-охотницы на демонов | KPop Demon Hunters (2025)]() 1:39:41
1:39:41
![Сверху вниз | Highest 2 Lowest (2025)]() 2:13:21
2:13:21
![Пакман в мире привидений]() 21:37
21:37
![Корги по имени Моко. Защитники планеты]() 4:33
4:33
![Псэмми. Пять детей и волшебство Сезон 1]() 12:17
12:17
![Сборники «Зебра в клеточку»]() 45:30
45:30
![Команда Дино. Исследователи Сезон 2]() 13:26
13:26
![Монсики]() 6:30
6:30
![Пиратская школа]() 11:06
11:06
![Школьный автобус Гордон]() 12:34
12:34
![Тодли Великолепный!]() 3:15
3:15
![Последний книжный магазин]() 11:20
11:20
![Команда Дино Сезон 1]() 12:08
12:08
![Агент 203]() 21:08
21:08
![Сборники «Оранжевая корова»]() 1:05:15
1:05:15
![Карли – искательница приключений. Древнее королевство]() 13:00
13:00
![Простоквашино]() 6:48
6:48
![Крутиксы]() 11:00
11:00
![Артур и дети круглого стола]() 11:22
11:22
![Таинственные золотые города]() 23:04
23:04
![Новое ПРОСТОКВАШИНО]() 6:30
6:30
![Панда и Антилопа]() 12:08
12:08

 1:45
1:45Скачать видео
| 256x144 | ||
| 432x232 | ||
| 640x360 | ||
| 856x480 | ||
| 1280x720 | ||
| 1920x1080 |
 5:45
5:45
2025-10-27 13:06
 4:01
4:01
2025-11-02 10:14
 4:00
4:00
2025-11-02 10:12
 3:36
3:36
2025-11-02 10:25
 2:39
2:39
2025-10-30 11:00
 3:33
3:33
2025-11-02 10:06
 4:04
4:04
2025-10-28 13:40
 3:20
3:20
2025-10-30 10:39
 4:27
4:27
2025-10-31 16:00
 2:13
2:13
2025-10-31 12:53
 2:29
2:29
2025-10-25 12:48
 3:25
3:25
2025-11-02 10:34
 3:10
3:10
2025-10-27 10:52
 2:37
2:37
2025-10-28 10:22
 2:24
2:24
2025-10-28 12:09
 4:26
4:26
2025-10-25 12:55
 3:59
3:59
2025-11-04 18:03
 3:56
3:56
2025-10-28 11:02
 2:49
2:49
2025-11-04 17:50
 2:18
2:18
2025-10-31 15:53
0/0
 2:05:43
2:05:43
2025-08-27 18:01
 1:34:38
1:34:38
2025-08-28 15:32
 1:46:45
1:46:45
2025-10-02 20:45
 1:54:40
1:54:40
2025-09-24 11:35
 1:31:23
1:31:23
2025-08-27 18:01
 1:50:38
1:50:38
2025-10-16 16:08
 2:09:55
2:09:55
2025-10-05 00:32
 1:25:47
1:25:47
2025-08-27 17:17
 2:57:46
2:57:46
2025-08-31 01:03
 1:38:22
1:38:22
2025-10-01 12:16
 1:27:40
1:27:40
2025-08-27 17:17
 1:29:27
1:29:27
2025-09-07 22:44
 1:26:24
1:26:24
2025-09-03 13:20
 2:36:13
2:36:13
2025-10-07 09:27
 1:44:57
1:44:57
2025-10-29 16:30
 1:42:60
1:42:60
2025-10-31 10:53
 1:46:40
1:46:40
2025-10-07 09:27
 1:42:50
1:42:50
2025-10-21 16:19
 1:39:41
1:39:41
2025-10-29 16:30
 2:13:21
2:13:21
2025-09-09 12:49
0/0
 21:37
21:37
2024-11-28 17:35
 4:33
4:33
2024-12-17 16:56
2021-09-22 22:23
 45:30
45:30
2025-09-17 18:49
2021-09-22 22:54
 6:30
6:30
2022-03-29 19:16
 11:06
11:06
2022-04-01 15:56
 12:34
12:34
2024-12-02 14:42
 3:15
3:15
2025-06-10 13:56
 11:20
11:20
2025-09-12 10:05
2021-09-22 22:29
 21:08
21:08
2025-01-09 16:39
 1:05:15
1:05:15
2025-09-30 13:45
 13:00
13:00
2024-11-28 16:19
 6:48
6:48
2025-10-17 10:00
 11:00
11:00
2022-07-25 18:59
 11:22
11:22
2023-05-11 14:51
 23:04
23:04
2025-01-09 17:26
 6:30
6:30
2018-04-03 10:35
 12:08
12:08
2025-06-10 14:59
0/0

